Benford's Law
If you take an ordinary list of numbers, such a list of the populations of cities, what is the probability that the first digit of each number is 1? The intuitive response is 1/9 working from the knowledge there are 9 possibilities (nothing starts with a 0) and the assumption that each digit should be equally like likely.
Oddly enough, it doesn't work that way. The chances of a 1 are around 30%, almost three times what one might expect. This phenomenon, known as Benford's Law, applies in all sorts of disparate cases (areas of rivers, constants, figures used in newspapers, debits in an accounting report, etc.). The distribution of starting digits is shown in the following chart.
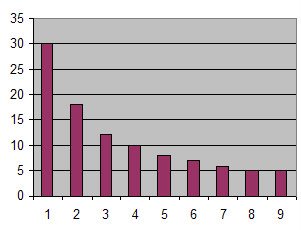
Finding an even distribution of starting digits can be a really good indicator of someone fudging the numbers.
Mathworld offers an in-depth explanation.
link
Oddly enough, it doesn't work that way. The chances of a 1 are around 30%, almost three times what one might expect. This phenomenon, known as Benford's Law, applies in all sorts of disparate cases (areas of rivers, constants, figures used in newspapers, debits in an accounting report, etc.). The distribution of starting digits is shown in the following chart.

Finding an even distribution of starting digits can be a really good indicator of someone fudging the numbers.
Mathworld offers an in-depth explanation.
link


0 Comments:
Post a Comment
Subscribe to Post Comments [Atom]
<< Home