What's the Area? (Part III)
This is Part 3 of a series discussing means of calculating area (here are links to 1 and 2). This time we're going to use calculus to calculate the area of the following trapezoid.
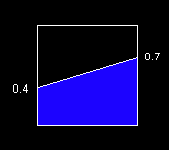
In order to do this, we'll figure out the height of the trapezoid as a function of x. The height begins at 0.4 and increases linearly by 0.3 across the unit square. The formula for height in slope-intercept form is...
y = 0.3*x + 0.4
Next, we integrate...
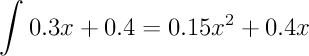
And evaluate the integral for the x in the range of [0,1]...

0.55. Calculus offers the same answer we found using geometry (i.e., looks like I didn't make any mistakes).
Q: When should we use it?
A: The calculus solution isn't as straightforward as the geometric solution; but, of course, if the top of our figure were some sort of curve, we'd probably need to move beyond geometry and on to calculus. When functions are hard or impossible to integrate, we'll need to use Simpson's Rule or Gaussian Quadrature or some other numerical integration technique. Lacking a formula for a curve, we might model the upper edge with a spline and integrate the spline to get an approximation of the actual area.
Pros: Calculus can give you answers where geometry can't.
Cons: Calculus isn't as easy as geometry.
Next, we're going to try the shotgun approach.

In order to do this, we'll figure out the height of the trapezoid as a function of x. The height begins at 0.4 and increases linearly by 0.3 across the unit square. The formula for height in slope-intercept form is...
y = 0.3*x + 0.4
Next, we integrate...
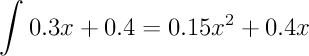
And evaluate the integral for the x in the range of [0,1]...

0.55. Calculus offers the same answer we found using geometry (i.e., looks like I didn't make any mistakes).
Q: When should we use it?
A: The calculus solution isn't as straightforward as the geometric solution; but, of course, if the top of our figure were some sort of curve, we'd probably need to move beyond geometry and on to calculus. When functions are hard or impossible to integrate, we'll need to use Simpson's Rule or Gaussian Quadrature or some other numerical integration technique. Lacking a formula for a curve, we might model the upper edge with a spline and integrate the spline to get an approximation of the actual area.
Pros: Calculus can give you answers where geometry can't.
Cons: Calculus isn't as easy as geometry.
Next, we're going to try the shotgun approach.


0 Comments:
Post a Comment
Subscribe to Post Comments [Atom]
<< Home