What's the Area? (Part IV)
This is Part 4 of a series discussing means of calculating area (here are links to 1, 2 and 3). In the near future I'm going discuss some numerical integration strategies.
Here we'll try what I like to call the shotgun approach to calculating the area of the trapezoid.

Let me explain what I mean by shotgun approach.
Imagine shooting a shotgun at our unit square and counting all of the resulting little holes. Multiply the percentage of the holes inside the trapezoid by the entire area of the bounding volume (in this case, the area of the unit square, which is 1).
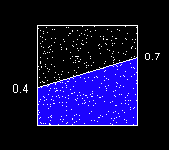
Will this work? Yup. How accurate will it be? It depends on how many little holes our shotgun blast creates.
Because I've had a horrible time getting decent indentation (non-breaking space) with Blogger, I put some sample code and output here: http://metamerist.com/code/shotgun.htm.
The code generates up to a million random points in the unit square and reports the area estimate for each iteration that's a power of 10, so you can get an idea of the rate of convergence.
The Shotgun Approach? That's just a name I like to use. The real name for this approach is Monte Carlo Integration.
Q: When should we use it?
A: In comparison to geometry and calculus, this seems like a rather haphazard means of calculating area. That said, one thing about this method is it doesn't require us to have knowledge of the precise boundaries of our area of interest. Monte Carlo Integration merely needs to know if a point is inside or outside. Monte Carlo Integration is one means integration (i.e., area or volume) when the exact boundaries are not known or the precise answer is not needed or the precise answer is hard to calculate. Generally, Monte Carlo is a last resort, but it's useful in integrating highly dimensional cases where options are limited.
Pros: Boundaries don't need to be known--only inside vs outside. It's an interative method that converges to the the solution, which gives one good control over a tradeoff between time and precision. Works with any number of dimensions.
Cons: Not precise. It converges very slowly and tends to be much more computationally intensive and less accurate than a geometric solution, calculus or other methods such as Simpson's Rule or Gaussian Quadrature.
Next, we'll try a peg board approach to Monte Carlo Integration...
Here we'll try what I like to call the shotgun approach to calculating the area of the trapezoid.

Let me explain what I mean by shotgun approach.
Imagine shooting a shotgun at our unit square and counting all of the resulting little holes. Multiply the percentage of the holes inside the trapezoid by the entire area of the bounding volume (in this case, the area of the unit square, which is 1).

Will this work? Yup. How accurate will it be? It depends on how many little holes our shotgun blast creates.
Because I've had a horrible time getting decent indentation (non-breaking space) with Blogger, I put some sample code and output here: http://metamerist.com/code/shotgun.htm.
The code generates up to a million random points in the unit square and reports the area estimate for each iteration that's a power of 10, so you can get an idea of the rate of convergence.
The Shotgun Approach? That's just a name I like to use. The real name for this approach is Monte Carlo Integration.
Q: When should we use it?
A: In comparison to geometry and calculus, this seems like a rather haphazard means of calculating area. That said, one thing about this method is it doesn't require us to have knowledge of the precise boundaries of our area of interest. Monte Carlo Integration merely needs to know if a point is inside or outside. Monte Carlo Integration is one means integration (i.e., area or volume) when the exact boundaries are not known or the precise answer is not needed or the precise answer is hard to calculate. Generally, Monte Carlo is a last resort, but it's useful in integrating highly dimensional cases where options are limited.
Pros: Boundaries don't need to be known--only inside vs outside. It's an interative method that converges to the the solution, which gives one good control over a tradeoff between time and precision. Works with any number of dimensions.
Cons: Not precise. It converges very slowly and tends to be much more computationally intensive and less accurate than a geometric solution, calculus or other methods such as Simpson's Rule or Gaussian Quadrature.
Next, we'll try a peg board approach to Monte Carlo Integration...


0 Comments:
Post a Comment
Subscribe to Post Comments [Atom]
<< Home