Linear Algebra for Graphics Geeks (Rotation)
Todd Will's excellent Introduction to the Singular Value Decomposition contains a some good insights regarding rotation matrices. Those insights are the inspiration behind this post.
Consider the 2x2 rotation matrix:
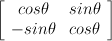
What's the result if we multiply by the identity matrix?
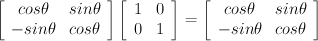
It's a silly question for anyone with a basic understanding of linear algebra. Multiplying by the identity matrix is the linear algebra equivalent of multiplying by one. Any matrix multiplied by the identity matrix is itself, A*I=A.
That said, let's look at things in a new light. Consider the rotation matrix transforming two column vectors, a unit vector on the x axis (1,0) and a unit vector on the y (0,1) axis:
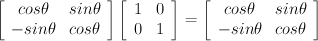
The funny thing is that this is the same problem--the matrix containing the two column vectors (1,0) and (0,1) is equal to the identity matrix.
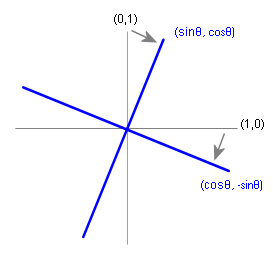
From the perspective of transforming these two column vectors, it's clear that the transformation rotates (1,0) into alignment with the first column vector and (0,1) into alignment with the second column vector.
Because the matrix is orthogonal, its inverse is its transpose. Multiplying the 2D rotation matrix by its transpose gives us:
The moral of the story is the effect of a matrix with an orthonormal basis in its column space. When the column vectors are orthogonal, the effect of the transformation is well understood by considering the transformation of the identity matrix, which is itself another orthonormal basis. The vector space represented by the identity matrix is rotated into alignment with the vector space defined by the orthonormal basis in the column vectors of the rotation matrix.
Another point for consideration is the effect of transposing the rotation matrix; the transpose of the rotation matrix is its inverse, and transposing it has the effect of turning the column vectors into row vectors; when the orthonormal basis of the column space is transposed into the row space, the effect is opposite that of the original matrix: the vector space defined by orthonormal basis in the row vectors is brought into alignment with the standard axes defined by the identity matrix.
Read more on Todd Will's page titled Perpframes, Aligners and Hangers. It's part of his tutorial on SVD, and it's a nice aid in comprehension.
This is post #11 of Linear Algebra for Graphics Geeks. Here are links to posts #1, #2, #3, #4, #5, #6, #7, #8, #9, #10.
Next, some notes on hand calculation of the SVD.
Consider the 2x2 rotation matrix:
What's the result if we multiply by the identity matrix?
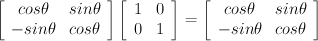
It's a silly question for anyone with a basic understanding of linear algebra. Multiplying by the identity matrix is the linear algebra equivalent of multiplying by one. Any matrix multiplied by the identity matrix is itself, A*I=A.
That said, let's look at things in a new light. Consider the rotation matrix transforming two column vectors, a unit vector on the x axis (1,0) and a unit vector on the y (0,1) axis:
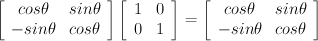
The funny thing is that this is the same problem--the matrix containing the two column vectors (1,0) and (0,1) is equal to the identity matrix.
From the perspective of transforming these two column vectors, it's clear that the transformation rotates (1,0) into alignment with the first column vector and (0,1) into alignment with the second column vector.

Because the matrix is orthogonal, its inverse is its transpose. Multiplying the 2D rotation matrix by its transpose gives us:
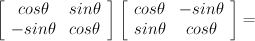
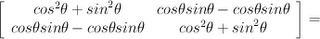
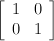
The moral of the story is the effect of a matrix with an orthonormal basis in its column space. When the column vectors are orthogonal, the effect of the transformation is well understood by considering the transformation of the identity matrix, which is itself another orthonormal basis. The vector space represented by the identity matrix is rotated into alignment with the vector space defined by the orthonormal basis in the column vectors of the rotation matrix.
Another point for consideration is the effect of transposing the rotation matrix; the transpose of the rotation matrix is its inverse, and transposing it has the effect of turning the column vectors into row vectors; when the orthonormal basis of the column space is transposed into the row space, the effect is opposite that of the original matrix: the vector space defined by orthonormal basis in the row vectors is brought into alignment with the standard axes defined by the identity matrix.
Read more on Todd Will's page titled Perpframes, Aligners and Hangers. It's part of his tutorial on SVD, and it's a nice aid in comprehension.
This is post #11 of Linear Algebra for Graphics Geeks. Here are links to posts #1, #2, #3, #4, #5, #6, #7, #8, #9, #10.
Next, some notes on hand calculation of the SVD.


0 Comments:
Post a Comment
Subscribe to Post Comments [Atom]
<< Home