Linear Algebra for Graphics Geeks (X'PDP'X)
After realizing I'd already covered much of yesterday's post, I decided to send it to the bone pile.
I feel I should be putting a disclaimer on many of these posts. The impetus behind my recent posts on linear algebra is the desire for a cerebral form of urban renewal. It's time to raze the crumbling buildings with broken windows and rebuild from the ground up as time permits.
And now today's experiment.
Given an angle theta, the following transformation rotates the the vectors (cos theta, sin theta) and (-sin theta, cos theta) into alignment with the x and y axes.

Given constants A and B, scale the results of the previous transformation.

Next, reverse the first rotation, putting the x and y axes back into alignment with theta.
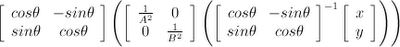
The net effect of these first three steps is scaling the world along the vector (cos theta, sin theta) and its normal vector (-sin theta, cos theta) by 1/A2 and 1/B2, respectively.
Now multiply everything by (x,y) as a row vector.

Rearrange the parens, which can be done because matrix multiplication is associative.
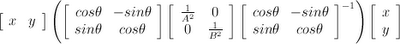
Impose the constraint that entire product must equal 1.

Finally, it's time to ask the question:
What have we here?
The answer is we have a matrix equation for an ellipse. It takes the following form:
XTQX = 1
Where Q corresponds to the (rotation * scale * rotation) in the final equation.
If theta is zero, the rotations become identity matrices, and it's easy to see that the product sans rotation is X2/A2 + Y2/B2 = 1.
The next point to make is that Q is an eigen decomposition.
Q = PDP-1
And, there's a beautiful symmetry to it all.
XT(PDP-1)X = 1
The question I'll leave to the reader is:
What's the transform that maps the unit circle into the ellipse described by this equation?
Collecting that idea and all the other ideas into a single example was a major objective here.
Please excuse any redundancies in these posts. When I think up examples I find insightful and I feel the inclination, those examples very well may show up here.
This is post #13* of Linear Algebra for Graphics Geeks. Here are links to posts #1, #2, #3, #4, #5, #6, #7, #8, #9, #10, #11, #12.
Next, more commentary on the subject of eigenvectors and the SVD.
I feel I should be putting a disclaimer on many of these posts. The impetus behind my recent posts on linear algebra is the desire for a cerebral form of urban renewal. It's time to raze the crumbling buildings with broken windows and rebuild from the ground up as time permits.
And now today's experiment.
Given an angle theta, the following transformation rotates the the vectors (cos theta, sin theta) and (-sin theta, cos theta) into alignment with the x and y axes.

Given constants A and B, scale the results of the previous transformation.

Next, reverse the first rotation, putting the x and y axes back into alignment with theta.
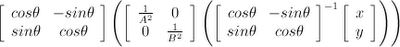
The net effect of these first three steps is scaling the world along the vector (cos theta, sin theta) and its normal vector (-sin theta, cos theta) by 1/A2 and 1/B2, respectively.
Now multiply everything by (x,y) as a row vector.

Rearrange the parens, which can be done because matrix multiplication is associative.
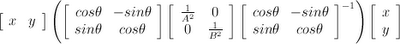
Impose the constraint that entire product must equal 1.

Finally, it's time to ask the question:
What have we here?
The answer is we have a matrix equation for an ellipse. It takes the following form:
XTQX = 1
Where Q corresponds to the (rotation * scale * rotation) in the final equation.
If theta is zero, the rotations become identity matrices, and it's easy to see that the product sans rotation is X2/A2 + Y2/B2 = 1.
The next point to make is that Q is an eigen decomposition.
Q = PDP-1
And, there's a beautiful symmetry to it all.
XT(PDP-1)X = 1
The question I'll leave to the reader is:
What's the transform that maps the unit circle into the ellipse described by this equation?
Collecting that idea and all the other ideas into a single example was a major objective here.
Please excuse any redundancies in these posts. When I think up examples I find insightful and I feel the inclination, those examples very well may show up here.
This is post #13* of Linear Algebra for Graphics Geeks. Here are links to posts #1, #2, #3, #4, #5, #6, #7, #8, #9, #10, #11, #12.
Next, more commentary on the subject of eigenvectors and the SVD.


0 Comments:
Post a Comment
Subscribe to Post Comments [Atom]
<< Home