Wednesday, January 31, 2007
Adobe is going to release Lightroom (congrats to friends, fellow Minneapolitans and the rest of the team). In other Adobe news, they're releasing PDF to ISO. Interesting piece in the New Yorker on Google's book scanning project (via 3QD). The Hobbit has been declared a new species of human. The Globe and Mail discusses a leaked draft of the impending IPCC report on global warming. Amazon finally hooked me into Amazon Prime with this sweet deal (pay $79 for 1 year but you get a gift certificate for $50 worth of groceries, which I would have bought anyway).
Sunday, January 28, 2007
Separated at Birth: McCain & Tigh?
As usual, Google shows my lack of originality in seeing similarities between Battlestar Galactica's Colonel Saul Tigh (played by Michael Hogan) and John McCain, but it hasn't stopped me from assembling the following collage (click for a larger view).


Saturday, January 27, 2007
Do you want a sample?
I'm a not a professional statistician, but that fact doesn't spare me from being repeatedly dumbstruck by invalid inferences made by people who should know better.
The most egregious errors are those stemming from bad population sampling. I've seen a lot of obliviousness when it comes to understanding the importance of random sampling and how misleading a biased sample can be.
Once I attended a presentation of a research study that concluded the majority of customers for a particular software company were corporate customers. This finding was completely contradictory to conventional wisdom within the company (technical support call demographics, representation on the Web, etc.).
When I asked about the evidence used to support the conclusion, the researcher revealed that the basis for the conclusion came from returned software registration cards. My next question asked if corporations might be more likely to register software than home users.
The researcher, chagrined, admitted the study assumed home users and corporate users were equally likely to register, but he had no basis for believing it, and it was a seriously flawed assumption.
Wikipedia notes a similar snafu in the history of statistical sampling:
"...[T]he 1936 Literary Digest prediction of a Republican win in the presidential election went badly awry, due to severe bias. A sample size of one million was obtained through magazine subscription lists and telephone directories. It was not appreciated that these lists were heavily biased towards Republicans and the resulting sample, though very large, was deeply flawed."
There's a right way and a wrong way to collect population sample data. The right way is to collect the data by randomly sampling the population. The wrong way is to simply let the data come to you. The data that come to you might not be representative of the general population.
If you only consider data coming to you, you might conclude the only sorts of people in the world are beggars and salesmen. Even if it's true in some profound sense, there are many other occupations.
The most egregious errors are those stemming from bad population sampling. I've seen a lot of obliviousness when it comes to understanding the importance of random sampling and how misleading a biased sample can be.
Once I attended a presentation of a research study that concluded the majority of customers for a particular software company were corporate customers. This finding was completely contradictory to conventional wisdom within the company (technical support call demographics, representation on the Web, etc.).
When I asked about the evidence used to support the conclusion, the researcher revealed that the basis for the conclusion came from returned software registration cards. My next question asked if corporations might be more likely to register software than home users.
The researcher, chagrined, admitted the study assumed home users and corporate users were equally likely to register, but he had no basis for believing it, and it was a seriously flawed assumption.
Wikipedia notes a similar snafu in the history of statistical sampling:
"...[T]he 1936 Literary Digest prediction of a Republican win in the presidential election went badly awry, due to severe bias. A sample size of one million was obtained through magazine subscription lists and telephone directories. It was not appreciated that these lists were heavily biased towards Republicans and the resulting sample, though very large, was deeply flawed."
There's a right way and a wrong way to collect population sample data. The right way is to collect the data by randomly sampling the population. The wrong way is to simply let the data come to you. The data that come to you might not be representative of the general population.
If you only consider data coming to you, you might conclude the only sorts of people in the world are beggars and salesmen. Even if it's true in some profound sense, there are many other occupations.
Friday, January 26, 2007
Tuesday, January 23, 2007
The Real Thing

One of the best blogs I read is Design Observer, and an extra round of applause goes to the excellent writing of Michael Bierut. Recently, he discussed "The It Factor" and Owen Edwards' book Quintessence:
"You know it when you see it. There's the iPod, and there are all those other MP3 players; there's the Louisville Slugger, and there are all those other baseball bats. As you've probably heard, Steve Jobs unveiled a long-awaited product last week; he intends to reduce the competition to nothing more than all those other phones.
What makes something the real thing? It's more than functionality, popularity, or beauty..."
link
Mother Teresa vs. Ayn Rand
SciAm writes about a study to be published in next month's Nature Neuroscience:
"WASHINGTON (Reuters) - Altruism, one of the most difficult human behaviors to define, can be detected in brain scans, U.S. researchers reported on Sunday.
They found activity in a specific area of the brain could predict altruistic behavior -- and people's own reports of how selfish or giving they are."
more
This continues a trend of philosophically troubling news from neuroscientists. Is it pointless to try to persuade some people to be kinder? How does one respond to the claim I'm not drawn that way?
Another philosophical implication of discoveries such as this is that, I believe, it strengthens the case of moral sense theorists such as Hutcheson, Hume, Smith and Locke--and in the modern day, thinkers such as E.O. Wilson.
"WASHINGTON (Reuters) - Altruism, one of the most difficult human behaviors to define, can be detected in brain scans, U.S. researchers reported on Sunday.
They found activity in a specific area of the brain could predict altruistic behavior -- and people's own reports of how selfish or giving they are."
more
This continues a trend of philosophically troubling news from neuroscientists. Is it pointless to try to persuade some people to be kinder? How does one respond to the claim I'm not drawn that way?
Another philosophical implication of discoveries such as this is that, I believe, it strengthens the case of moral sense theorists such as Hutcheson, Hume, Smith and Locke--and in the modern day, thinkers such as E.O. Wilson.
Monday, January 22, 2007
MMVI, the post that never was...
I planned on doing a 2006 favorites post, but never found the time, so in the interest of brevity... on the subject of music, here are three four discs I discovered in '06 that I find worthy of recommendation...
1. Corinne Bailey Rae - self titled. Although I listen to the radio very little, even I couldn't manage to miss Put Your Records On, but things don't end there--it really is a nice disc.
2. Imogen Heap - Speak for Yourself. Although it was released in November 2005, it's still on the list. Both Imogen Heap and Corinne Bailey Rae have been nominated for the Grammy for best new artist. Here's a link to Goodnight and Go on YouTube.
3. Jose Gonzalez - Veneer. Remember the excellent tune playing in the Sony Bravia bouncing ball commercial? The song was Heartbeats from this fine release. (Yes, this was originally released in the second half of 2005 too.)
4. Lou Rhodes - Beloved One, mentioned previously.
Note: Honorable mention goes to Regina Spektor for Begin to Hope. Sample: Better.
1. Corinne Bailey Rae - self titled. Although I listen to the radio very little, even I couldn't manage to miss Put Your Records On, but things don't end there--it really is a nice disc.
2. Imogen Heap - Speak for Yourself. Although it was released in November 2005, it's still on the list. Both Imogen Heap and Corinne Bailey Rae have been nominated for the Grammy for best new artist. Here's a link to Goodnight and Go on YouTube.
3. Jose Gonzalez - Veneer. Remember the excellent tune playing in the Sony Bravia bouncing ball commercial? The song was Heartbeats from this fine release. (Yes, this was originally released in the second half of 2005 too.)
4. Lou Rhodes - Beloved One, mentioned previously.
Note: Honorable mention goes to Regina Spektor for Begin to Hope. Sample: Better.
Sunday, January 21, 2007
Prodigies
In 1909, four prodigies enrolled at Harvard. Adolf Augustus Berle (14), Cedric Wing Huffington (15), William James Sidis (11) and Norbert Weiner (14). Roger Sessions (14) appeared a year later in 1910. The phenomenon didn't escape media attention; they were pretty well dogged by the press.
In light of prodigy films of recent years, I think the collective story of these prodigies could make for a great film. In fact, there's a great film to be made just in the telling of the story of William James Sidis alone. If you're unfamiliar, a little Googling is recommended. There are also some interesting links at the end of the Wikipedia entry on Sidis.
One of the books I currently have in heavy rotation is Dark Hero of the Information Age: In Search of Norbert Weiner The Father of Cybernetics, and from it I've learned a number of interesting things about Weiner. I didn't realize he'd studied under so many great minds, including Bertrand Russell, G.H. Hardy, David Hilbert, Henri Lebesgue, Edmund Husserl and others. According to the book, Hardy really helped in opening Weiner's eyes to higher mathematics (pb. 32)
Weiner's story is yet another instance of a prodigy who was driven too hard by a highly-educated, overbearing father. I'm not sure how many times I've seen this, but the stories of John Stuart Mill and William James Sidis come immediately to mind.
Finally, in the process of researching the subject of prodigies, I found this page on Michael Kearney, who, if true, even surpassed Sidis in early language skills: "He spoke his first words at four months. At the age of six months, he said to his pediatrician "I have a left ear infection" [1] and learned to read at the age of ten months. [2]"
Jinkies.
In light of prodigy films of recent years, I think the collective story of these prodigies could make for a great film. In fact, there's a great film to be made just in the telling of the story of William James Sidis alone. If you're unfamiliar, a little Googling is recommended. There are also some interesting links at the end of the Wikipedia entry on Sidis.
One of the books I currently have in heavy rotation is Dark Hero of the Information Age: In Search of Norbert Weiner The Father of Cybernetics, and from it I've learned a number of interesting things about Weiner. I didn't realize he'd studied under so many great minds, including Bertrand Russell, G.H. Hardy, David Hilbert, Henri Lebesgue, Edmund Husserl and others. According to the book, Hardy really helped in opening Weiner's eyes to higher mathematics (pb. 32)
Weiner's story is yet another instance of a prodigy who was driven too hard by a highly-educated, overbearing father. I'm not sure how many times I've seen this, but the stories of John Stuart Mill and William James Sidis come immediately to mind.
Finally, in the process of researching the subject of prodigies, I found this page on Michael Kearney, who, if true, even surpassed Sidis in early language skills: "He spoke his first words at four months. At the age of six months, he said to his pediatrician "I have a left ear infection" [1] and learned to read at the age of ten months. [2]"
Jinkies.
Saturday, January 20, 2007
Hate it when that happens...
Today's Minneapolis Star Tribune:
"A 29-year-old man who was apparently horsing around with some friends crashed through a window and fell nearly 17 stories at the downtown Minneapolis Hyatt Regency early this morning. His most severe injury? A broken leg."
Man, I hate it when that happens. It really is one of the worst ways to break a leg.
link
"A 29-year-old man who was apparently horsing around with some friends crashed through a window and fell nearly 17 stories at the downtown Minneapolis Hyatt Regency early this morning. His most severe injury? A broken leg."
Man, I hate it when that happens. It really is one of the worst ways to break a leg.
link
Wednesday, January 17, 2007
Gaussian Integral Approximations
In the ongoing debate over the veracity and utility of Wikipedia, I noticed one critic claiming Wikipedia tends to be better with highly technical articles, because interest is limited to an elite few. This is an observation that squares with my own experience. When it comes to questions mathematical, I often even find Wikipedia superior to MathWorld, with the former frequently going into greater length and detail than the latter.

As far as things mathematical go, I have noticed many a Wiki entry referencing Handbook of the Mathematical Functions, edited by Irene Stegun and Milton Abramowitz from the National Bureau of Standards. It's an older reference (last printed in '72), but it's in the public domain, and it's available online in scanned form (here, for example).
After finding the +900 pages of online scans a little unwieldy, I decided to simply get a copy, which can be had in paperback from used book sites for as little as ten bucks, shipping included. "Designed to provide scientific investigators with a comprehensive and self-contained summary of the mathematical functions that arise in physical and engineering problems," it contains a lot of useful information. For example, there are some great approximations in it, such as those for the Gaussian Integral here on page 932.
And this brings us to the second part of this post.
A while back, I was playing with some different means of calculating the Gaussian Integral. First, I searched for an extremely accurate version to serve as a baseline. I turned to W.J. Cody's ERF function, found in ACM Algorithm 462, which claims accuracy of 18 significant digits.
Yes, this involved FORTRAN spelunking. I cranked up f2c for the first time in a long time. While the conversion seemed to go fine, my outputs indicated something somewhere went wrong. A brief attempt at compiling with gfortran exceeded my limited patience, so in the end I wound up porting it by hand. (In retrospect, I should have recorded a Visual Studio macro while busily changing ".LE." to "<=", etc.)
In the end, thanks to Cody, Stegun and Abramowitz, I coded up four different approximations for the Gaussian Integral. The implementations are available with results for perusal here.

As far as things mathematical go, I have noticed many a Wiki entry referencing Handbook of the Mathematical Functions, edited by Irene Stegun and Milton Abramowitz from the National Bureau of Standards. It's an older reference (last printed in '72), but it's in the public domain, and it's available online in scanned form (here, for example).
After finding the +900 pages of online scans a little unwieldy, I decided to simply get a copy, which can be had in paperback from used book sites for as little as ten bucks, shipping included. "Designed to provide scientific investigators with a comprehensive and self-contained summary of the mathematical functions that arise in physical and engineering problems," it contains a lot of useful information. For example, there are some great approximations in it, such as those for the Gaussian Integral here on page 932.
And this brings us to the second part of this post.
A while back, I was playing with some different means of calculating the Gaussian Integral. First, I searched for an extremely accurate version to serve as a baseline. I turned to W.J. Cody's ERF function, found in ACM Algorithm 462, which claims accuracy of 18 significant digits.
Yes, this involved FORTRAN spelunking. I cranked up f2c for the first time in a long time. While the conversion seemed to go fine, my outputs indicated something somewhere went wrong. A brief attempt at compiling with gfortran exceeded my limited patience, so in the end I wound up porting it by hand. (In retrospect, I should have recorded a Visual Studio macro while busily changing ".LE." to "<=", etc.)
In the end, thanks to Cody, Stegun and Abramowitz, I coded up four different approximations for the Gaussian Integral. The implementations are available with results for perusal here.
Tuesday, January 16, 2007
Notation x 3

Jim Blinn's Notation, Notation, Notation is one of the books I've been picking up lately when I find time to read. Reading Blinn is both enlightening and humbling; his mathematical expositions are extraordinarily lucid and insightful.
Like his previous two books, Notation, Notation, Notation is a collection of articles written for his column in IEEE Computer Graphics and Applications.
This edition contains a highly recommended 1996 article, Consider the Lowly 2x2 Matrix, and it offers many valuable and important insights into linear algebra in its consideration of 2x2 matrices. I wish I could have read this before I took linear algebra.
The Grandfather of PostScript?
An interesting post at Sean Gleeson:
"In 1535 A.D., German artist Albrecht Durer invented computer fonts. Well, no, not really. But he would have. I'll explain..."
"Durer didn't have a computer. But for some reason (those were some crazy days) he thought it would be a good idea to describe how to draft all the letters of the Roman alphabet, using only geometric terms such as 'square,' 'circle,' and 'line.' These instructions were published in 1535 as Of the Just Shaping of Letters..."
Gleason's post includes a scan of a PDF version of Durer's work.
link
(ht: Brainwagon)
"In 1535 A.D., German artist Albrecht Durer invented computer fonts. Well, no, not really. But he would have. I'll explain..."
"Durer didn't have a computer. But for some reason (those were some crazy days) he thought it would be a good idea to describe how to draft all the letters of the Roman alphabet, using only geometric terms such as 'square,' 'circle,' and 'line.' These instructions were published in 1535 as Of the Just Shaping of Letters..."
Gleason's post includes a scan of a PDF version of Durer's work.
link
(ht: Brainwagon)
Sunday, January 14, 2007
3D Morphable Model Face Animation
Nice work in the parameterization of human facial features. Definitely worth a watch.
(via John Nack)
(via John Nack)
Thursday, January 11, 2007
Lou Rhodes
I'm beginning to realize how this blog works. When I'm too busy to write something more substantial, I often do a musical post. What's both surprising and interesting to me is that these tend to get a lot of views. If I can introduce a single person to a single piece of new music they come to love, I'll consider all efforts a success.
The first Lamb song that really attracted my attention was Gorecki (YouTube), inspired by Henryk Gorecki's Third Symphony. There's something really compelling about Lou Rhodes' voice and Lamb's style. If you're unfamiliar, another one of their most popular songs is Gabriel (YouTube).
Of all of the discs nominated for the 2006 Mercury Prize, Lou's Beloved One is my favorite. Maybe I need to give the Arctic Monkeys more of a chance--maybe I'm just a contrarian at heart. Finally, here's a link to my favorite song off her latest disc, an excellent tune called Tremble...
The first Lamb song that really attracted my attention was Gorecki (YouTube), inspired by Henryk Gorecki's Third Symphony. There's something really compelling about Lou Rhodes' voice and Lamb's style. If you're unfamiliar, another one of their most popular songs is Gabriel (YouTube).
Of all of the discs nominated for the 2006 Mercury Prize, Lou's Beloved One is my favorite. Maybe I need to give the Arctic Monkeys more of a chance--maybe I'm just a contrarian at heart. Finally, here's a link to my favorite song off her latest disc, an excellent tune called Tremble...
First Dates
Out to dinner last night, noisy P.F. Chang's, wound up seated next to what seemed to be Andrew Dice Clay's younger brother on a first date...
He: "So how is things goin' wit' work?"
She: "Work really sucks!"
He: "So... yooze in jail, huh?"
She: "Huh?"
He: "You just said work release sucks..."
She: "No, work really sucks!"
Misty water-colored memories...
He: "So how is things goin' wit' work?"
She: "Work really sucks!"
He: "So... yooze in jail, huh?"
She: "Huh?"
He: "You just said work release sucks..."
She: "No, work really sucks!"
Misty water-colored memories...
Wednesday, January 10, 2007
The Camera Doesn't Lie

Shortly after he made the jump, my younger son fell off the sled to be left supine on the ground in tears. I thought he was crying because he wiped out, but he claimed his older brother hit him with a snowball. While reviewing my shots from Christmas, I realized I'd recorded the crime. Note the niveous shrapnel flying off the victim's head. Man, he really pasted him!
I was shooting in multi-shot mode. The previous frame shows big brother surreptitiously in wait with icy projectile...

Kids.
The Ideological Animal
"We think our political stance is the product of reason, but we're easily manipulated and surprisingly malleable. Our essential political self is more a stew of childhood temperament, education, and fear of death. Call it the 9/11 effect."
Jay Dixit writes an interesting article on political bias in Psychology Today.
(ht:3QD)
Note: The more science reveals, the more my respect for David Hume grows...
"Reason is and ought to be the slave of the passions and can never pretend to any other office than to serve and obey them." -- David Hume, A Treatise on Human Nature.
Jay Dixit writes an interesting article on political bias in Psychology Today.
(ht:3QD)
Note: The more science reveals, the more my respect for David Hume grows...
"Reason is and ought to be the slave of the passions and can never pretend to any other office than to serve and obey them." -- David Hume, A Treatise on Human Nature.
Do you like Apples?

The world's abuzz with the Apple's iPhone and iTV revelations. It's interesting Apple Computer, Inc. is dropping the "Computer" to become Apple, Inc.
In other Apple news, Cabel looks at an Apple patent on resizable user interfaces by Mark Zimmer:
"Here's the deal with this patent: Apple's approach seems is far more interesting, and ultimately more amazing. In essence, they're creating a user interface that's completely programmatically defined. I.e., not an exported series of graphic resources, but a series of instructions that define how the graphics should be drawn, from the ground up"
Periodic Table of Visualization
Even though this has already been BoingBoing-ed, the Periodic Table of Visualization Methods at Visual-Literacy.org is worth noting.


Tuesday, January 09, 2007
The Overzealous Boy Scout
There's the story of the boy scout who helped the little old lady across the street--even though she didn't want to go. We seem to be getting too much software that falls into this category (and another category I call "Dumbware," but that's another post).
Here's how my ideal Netflix workflow would go...
1. I find a movie I want to watch.
2. I add that movie to my queue.
3. Lather, rinse and repeat.
Here's how my Netflix workflow actually goes...
1. I find a movie I want to watch.
2. I add it to my queue.
3. An Overzealous Boy Scout appears recommending movies I should like.
4. I close the antihelpful O.B.S. popup.
5. Lather, rinse and repeat.
Five movies. Five overzealous boy scouts batted out of the way.
While I'm on the subject, there's the issue of whether fresh Netflix Queue additions should wind up in the bottom of the queue or the top. Presenting two buttons, "Add to top of queue" and "Add to bottom of queue," would save another step. If designers believe this would be too confusing for users, we may be stumbling onto one of the root causes of Dumbware (but that's another post).
Here's how my ideal Netflix workflow would go...
1. I find a movie I want to watch.
2. I add that movie to my queue.
3. Lather, rinse and repeat.
Here's how my Netflix workflow actually goes...
1. I find a movie I want to watch.
2. I add it to my queue.
3. An Overzealous Boy Scout appears recommending movies I should like.
4. I close the antihelpful O.B.S. popup.
5. Lather, rinse and repeat.
Five movies. Five overzealous boy scouts batted out of the way.
While I'm on the subject, there's the issue of whether fresh Netflix Queue additions should wind up in the bottom of the queue or the top. Presenting two buttons, "Add to top of queue" and "Add to bottom of queue," would save another step. If designers believe this would be too confusing for users, we may be stumbling onto one of the root causes of Dumbware (but that's another post).
Saturday, January 06, 2007
The Birds and the Bees
And now for something completely different...
I'm quite certain Patrick Dawes & Eugene Bazodis share a relatively recent common ancestor with the late Tiny Tim.
(Note: One failure of Google, imho, is that it's often difficult to find the actual web site of businesses--especially restaurants--because reviews wind up with higher PageRank than the actual establishments themselves. Please disregard the following attempt to boost the PageRank of one of my favorite restaurants: Thistle's Restaurant.)
I'm quite certain Patrick Dawes & Eugene Bazodis share a relatively recent common ancestor with the late Tiny Tim.
(Note: One failure of Google, imho, is that it's often difficult to find the actual web site of businesses--especially restaurants--because reviews wind up with higher PageRank than the actual establishments themselves. Please disregard the following attempt to boost the PageRank of one of my favorite restaurants: Thistle's Restaurant.)
What's the Area? (Part VI)
This is Part 6 of a series on calculating area and integration. In the first part, I introduced the problem. In the second part, I used geometry to calculate the area of a trapezoid. In Part 3, we looked to calculus for a solution. In Part 4, we employed a shotgun approach and randomly sampled the space for Monte Carlo integration. In Part 5, we tried uniform sampling (the peg board approach) and found it didn't work as well as random sampling.
An impetus behind writing this series involves the relationship between theory and practice and how the two are typically taught. Theory often seems to run East and West while practice runs North and South. When one learns geometry, one learns all of the ins and outs of geometry. So it goes with calculus, statistics, numerical methods, etc.
In education and inquiry, topics are typically addressed along the "theory axis," and issues are rarely addressed along the "practice axis" due to the dynamics of specialization. Your best bet for a course discussing along the practice axis might be a course in applied mathematics or numerical methods or mathematics for engineers. For me this series of posts is an initial experiment in looking at a simple problem and trying to examine it along the axis of practice with a comparative approach.
After trying the shotgun approach and the peg board approach to Monte Carlo, I closed asking if there's a better way to sample the space. The answer comes in a technique called Quasi-Monte Carlo Integration.
In the sampling of space in Monte Carlo Integration (what I called the shotgun approach), random points were selected using pseudo-random numbers. If you don't know what pseudo-random numbers are, it will have to suffice to say these are fake random numbers generated by computers that are for most practical purposes just as good as the real thing. Computers, being deterministic, can't generate random numbers in the traditional sense of the word. (What random means exactly is a whole other philosophical abyss that will be quite intentionally avoided here.)
While Monte Carlo Integration uses pseudo-random numbers to generate sample points, Quasi-Monte Carlo uses quasi-random numbers. One thing about quasi-random numbers is that they're among the most poorly named mathematical entities, so perhaps you should erase the term quasi-random from memory now and learn to call them low discrepancy sequences from the beginning (although the Wikipedia entry is tagged as being in need of expert attention, it still has interesting information in it).
One of the simplest quasi-random / low discrepancy sequences is the Halton sequence, named after John H. Halton. I've chosen the Halton sequence as an example because it is simply explained, my intention is only to demonstrate a general principle, and I don't think I'll have time to do anything more than list the names of other low discrepancy sequences (cf. Hammersley, Sobol, Faure, Neiderreiter).
To generate the Halton sequence, convert a number from base 10 to a prime number base, mirror the number about the decimal point, and finally convert the number back to base 10.
An example is illuminating. Let's use base 2, because it's familiar to computer geeks and bits are computationally attractive.
1 -> 001.0 -> 0.100 -> 0.500
2 -> 010.0 -> 0.010 -> 0.250
3 -> 011.0 -> 0.110 -> 0.750
4 -> 100.0 -> 0.010 -> 0.125
5 -> 101.0 -> 0.101 -> 0.625
6 -> 110.0 -> 0.011 -> 0.375
7 -> 111.0 -> 0.111 -> 0.875
If you examine the sequence for a while, you'll see why quasi-random is a poor name. In the case of base 2, the first point is in the middle, the next is half way between the middle and the lower bound, the next is half way between the middle and the upper bound, etc. Similar results are found with other bases.
It's quite beautiful in terms of simplicity and results. If you think about the problems we encountered with the peg board approach of uniform sampling, you should see the value in using low discrepancy sequences for sampling.
Quasi-random sequences tend to converge more quickly than uniform sampling (the peg board approach) and pseudo-random sequences (the shotgun approach), and they're more orderly than pseudo-random sequences (which is why low discrepancy is a better term than quasi-random).
Here's a nice page at FSU with links to 2D plots of sample points resulting from quasi-random sequences in the unit square. (Also: Here's a little applet I cranked out [i.e., may contain bugs, but seems to match Burkardt's page] that demonstrates 2D points using the Halton sequence [base 2 for x and base 3 for y].)
At this point, I feel I'm beginning to deviate from the subject of calculating area and integration into the subject of point samping. Oh well, this is useful stuff to know and applicable in many areas from computer graphics to stochastic geometry to statistical mechanics to financial engineering.
An impetus behind writing this series involves the relationship between theory and practice and how the two are typically taught. Theory often seems to run East and West while practice runs North and South. When one learns geometry, one learns all of the ins and outs of geometry. So it goes with calculus, statistics, numerical methods, etc.
In education and inquiry, topics are typically addressed along the "theory axis," and issues are rarely addressed along the "practice axis" due to the dynamics of specialization. Your best bet for a course discussing along the practice axis might be a course in applied mathematics or numerical methods or mathematics for engineers. For me this series of posts is an initial experiment in looking at a simple problem and trying to examine it along the axis of practice with a comparative approach.
After trying the shotgun approach and the peg board approach to Monte Carlo, I closed asking if there's a better way to sample the space. The answer comes in a technique called Quasi-Monte Carlo Integration.
In the sampling of space in Monte Carlo Integration (what I called the shotgun approach), random points were selected using pseudo-random numbers. If you don't know what pseudo-random numbers are, it will have to suffice to say these are fake random numbers generated by computers that are for most practical purposes just as good as the real thing. Computers, being deterministic, can't generate random numbers in the traditional sense of the word. (What random means exactly is a whole other philosophical abyss that will be quite intentionally avoided here.)
While Monte Carlo Integration uses pseudo-random numbers to generate sample points, Quasi-Monte Carlo uses quasi-random numbers. One thing about quasi-random numbers is that they're among the most poorly named mathematical entities, so perhaps you should erase the term quasi-random from memory now and learn to call them low discrepancy sequences from the beginning (although the Wikipedia entry is tagged as being in need of expert attention, it still has interesting information in it).
One of the simplest quasi-random / low discrepancy sequences is the Halton sequence, named after John H. Halton. I've chosen the Halton sequence as an example because it is simply explained, my intention is only to demonstrate a general principle, and I don't think I'll have time to do anything more than list the names of other low discrepancy sequences (cf. Hammersley, Sobol, Faure, Neiderreiter).
To generate the Halton sequence, convert a number from base 10 to a prime number base, mirror the number about the decimal point, and finally convert the number back to base 10.
An example is illuminating. Let's use base 2, because it's familiar to computer geeks and bits are computationally attractive.
1 -> 001.0 -> 0.100 -> 0.500
2 -> 010.0 -> 0.010 -> 0.250
3 -> 011.0 -> 0.110 -> 0.750
4 -> 100.0 -> 0.010 -> 0.125
5 -> 101.0 -> 0.101 -> 0.625
6 -> 110.0 -> 0.011 -> 0.375
7 -> 111.0 -> 0.111 -> 0.875
If you examine the sequence for a while, you'll see why quasi-random is a poor name. In the case of base 2, the first point is in the middle, the next is half way between the middle and the lower bound, the next is half way between the middle and the upper bound, etc. Similar results are found with other bases.
It's quite beautiful in terms of simplicity and results. If you think about the problems we encountered with the peg board approach of uniform sampling, you should see the value in using low discrepancy sequences for sampling.
Quasi-random sequences tend to converge more quickly than uniform sampling (the peg board approach) and pseudo-random sequences (the shotgun approach), and they're more orderly than pseudo-random sequences (which is why low discrepancy is a better term than quasi-random).
Here's a nice page at FSU with links to 2D plots of sample points resulting from quasi-random sequences in the unit square. (Also: Here's a little applet I cranked out [i.e., may contain bugs, but seems to match Burkardt's page] that demonstrates 2D points using the Halton sequence [base 2 for x and base 3 for y].)
At this point, I feel I'm beginning to deviate from the subject of calculating area and integration into the subject of point samping. Oh well, this is useful stuff to know and applicable in many areas from computer graphics to stochastic geometry to statistical mechanics to financial engineering.
Thursday, January 04, 2007
What's the Area? (Part V)
This is Part 5 of a series discussing methods of integration (here are links to 1, 2, 3 and 4). The last post looked at a case of Monte Carlo Integration, which amounted to a shotgun approach in which the proportion of random points falling inside the boundaries of a trapezoid was used to estimate its area.
Although it's called Monte Carlo, this numerical integration strategy doesn't require points to be selected randomly. Other sampling methods can be employed with varying results.
Although sequential, uniform sampling is standard and works well in areas such as digital signal processing, it doesn't typically work well with Monte Carlo Integration (for reasons that may be obvious).
Given my calling the previous case the shotgun approach, the case of uniform sampling strategy might be called the peg board approach...

I ran a test sampling uniformly from left to right and top to bottom. Due to the fact the trapezoid occupies mostly the bottom half of the unit cube, things don't get close to the magic 0.55 until we've sampled the most of the space... (please excuse Blogger's lack of support for decent indentation)...
iterations estimate relative error
---------- -------- --------------
10^1 1.000000 0.818182
10^2 1.000000 0.818182
10^3 1.000000 0.818182
10^4 1.000000 0.818182
10^5 1.000000 0.818182
10^6 0.550398 0.000724
(Note: this is a case where a logarithmic scale for sample count really doesn't tell the story very well. A linear scale of 100,000 per step would demonstrate things better with gradual linear improvements from 100,000 to 1,000,000.)
In comparison, here are the results we obtained through random sampling...
iterations estimate relative error
---------- -------- --------------
10^1 0.500000 0.090909
10^2 0.530000 0.036364
10^3 0.510000 0.072727
10^4 0.540500 0.017273
10^5 0.549610 0.000709
10^6 0.550114 0.000207
Uniform sampling didn't work well. Random sampling worked better. Are there even better means of sampling the space? This question brings us to the point where I think the problem becomes much more interesting.
In Part 6, we'll find an answer.
Although it's called Monte Carlo, this numerical integration strategy doesn't require points to be selected randomly. Other sampling methods can be employed with varying results.
Although sequential, uniform sampling is standard and works well in areas such as digital signal processing, it doesn't typically work well with Monte Carlo Integration (for reasons that may be obvious).
Given my calling the previous case the shotgun approach, the case of uniform sampling strategy might be called the peg board approach...

I ran a test sampling uniformly from left to right and top to bottom. Due to the fact the trapezoid occupies mostly the bottom half of the unit cube, things don't get close to the magic 0.55 until we've sampled the most of the space... (please excuse Blogger's lack of support for decent indentation)...
iterations estimate relative error
---------- -------- --------------
10^1 1.000000 0.818182
10^2 1.000000 0.818182
10^3 1.000000 0.818182
10^4 1.000000 0.818182
10^5 1.000000 0.818182
10^6 0.550398 0.000724
(Note: this is a case where a logarithmic scale for sample count really doesn't tell the story very well. A linear scale of 100,000 per step would demonstrate things better with gradual linear improvements from 100,000 to 1,000,000.)
In comparison, here are the results we obtained through random sampling...
iterations estimate relative error
---------- -------- --------------
10^1 0.500000 0.090909
10^2 0.530000 0.036364
10^3 0.510000 0.072727
10^4 0.540500 0.017273
10^5 0.549610 0.000709
10^6 0.550114 0.000207
Uniform sampling didn't work well. Random sampling worked better. Are there even better means of sampling the space? This question brings us to the point where I think the problem becomes much more interesting.
In Part 6, we'll find an answer.
Shuffling, semantics and desires
A while back I ran into this piece by Steven Levy: Does Your iPod Play Favorites? I planned on a writing post about it, but I forgot until today.
The article addresses the fact that when the iPod Shuffle randomizes a playlist, it's frequently the case for a shuffled playlist to include three songs in a row by the same artist. Apple's engineers and a Temple university professor assure Levy the iPod is shuffling just fine--the resulting playlist is indeed random--but what's not addressed in the article is that as far as the shuffling goes, semantics aside, there's still a gap between a randomly shuffled playlist and what is actually desired.
When we say we want our songs shuffled, what we want is not merely a random shuffling in a mathematical or algorithmic sense, and assurances that the playlist is randomly shuffled do little to solve the problem. What we want is more restrictive. Like Levy, we want a shuffled playlist the doesn't contain multiple tracks in a row from the same artist (or possibly the same disc). Given the presence of artist and album information and a sufficiently diverse playlist, it shouldn't be hard to enforce this additional constraint on the resulting playlist.
The article addresses the fact that when the iPod Shuffle randomizes a playlist, it's frequently the case for a shuffled playlist to include three songs in a row by the same artist. Apple's engineers and a Temple university professor assure Levy the iPod is shuffling just fine--the resulting playlist is indeed random--but what's not addressed in the article is that as far as the shuffling goes, semantics aside, there's still a gap between a randomly shuffled playlist and what is actually desired.
When we say we want our songs shuffled, what we want is not merely a random shuffling in a mathematical or algorithmic sense, and assurances that the playlist is randomly shuffled do little to solve the problem. What we want is more restrictive. Like Levy, we want a shuffled playlist the doesn't contain multiple tracks in a row from the same artist (or possibly the same disc). Given the presence of artist and album information and a sufficiently diverse playlist, it shouldn't be hard to enforce this additional constraint on the resulting playlist.
Wednesday, January 03, 2007
What's the Area? (Part IV)
This is Part 4 of a series discussing means of calculating area (here are links to 1, 2 and 3). In the near future I'm going discuss some numerical integration strategies.
Here we'll try what I like to call the shotgun approach to calculating the area of the trapezoid.

Let me explain what I mean by shotgun approach.
Imagine shooting a shotgun at our unit square and counting all of the resulting little holes. Multiply the percentage of the holes inside the trapezoid by the entire area of the bounding volume (in this case, the area of the unit square, which is 1).
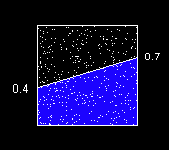
Will this work? Yup. How accurate will it be? It depends on how many little holes our shotgun blast creates.
Because I've had a horrible time getting decent indentation (non-breaking space) with Blogger, I put some sample code and output here: http://metamerist.com/code/shotgun.htm.
The code generates up to a million random points in the unit square and reports the area estimate for each iteration that's a power of 10, so you can get an idea of the rate of convergence.
The Shotgun Approach? That's just a name I like to use. The real name for this approach is Monte Carlo Integration.
Q: When should we use it?
A: In comparison to geometry and calculus, this seems like a rather haphazard means of calculating area. That said, one thing about this method is it doesn't require us to have knowledge of the precise boundaries of our area of interest. Monte Carlo Integration merely needs to know if a point is inside or outside. Monte Carlo Integration is one means integration (i.e., area or volume) when the exact boundaries are not known or the precise answer is not needed or the precise answer is hard to calculate. Generally, Monte Carlo is a last resort, but it's useful in integrating highly dimensional cases where options are limited.
Pros: Boundaries don't need to be known--only inside vs outside. It's an interative method that converges to the the solution, which gives one good control over a tradeoff between time and precision. Works with any number of dimensions.
Cons: Not precise. It converges very slowly and tends to be much more computationally intensive and less accurate than a geometric solution, calculus or other methods such as Simpson's Rule or Gaussian Quadrature.
Next, we'll try a peg board approach to Monte Carlo Integration...
Here we'll try what I like to call the shotgun approach to calculating the area of the trapezoid.

Let me explain what I mean by shotgun approach.
Imagine shooting a shotgun at our unit square and counting all of the resulting little holes. Multiply the percentage of the holes inside the trapezoid by the entire area of the bounding volume (in this case, the area of the unit square, which is 1).

Will this work? Yup. How accurate will it be? It depends on how many little holes our shotgun blast creates.
Because I've had a horrible time getting decent indentation (non-breaking space) with Blogger, I put some sample code and output here: http://metamerist.com/code/shotgun.htm.
The code generates up to a million random points in the unit square and reports the area estimate for each iteration that's a power of 10, so you can get an idea of the rate of convergence.
The Shotgun Approach? That's just a name I like to use. The real name for this approach is Monte Carlo Integration.
Q: When should we use it?
A: In comparison to geometry and calculus, this seems like a rather haphazard means of calculating area. That said, one thing about this method is it doesn't require us to have knowledge of the precise boundaries of our area of interest. Monte Carlo Integration merely needs to know if a point is inside or outside. Monte Carlo Integration is one means integration (i.e., area or volume) when the exact boundaries are not known or the precise answer is not needed or the precise answer is hard to calculate. Generally, Monte Carlo is a last resort, but it's useful in integrating highly dimensional cases where options are limited.
Pros: Boundaries don't need to be known--only inside vs outside. It's an interative method that converges to the the solution, which gives one good control over a tradeoff between time and precision. Works with any number of dimensions.
Cons: Not precise. It converges very slowly and tends to be much more computationally intensive and less accurate than a geometric solution, calculus or other methods such as Simpson's Rule or Gaussian Quadrature.
Next, we'll try a peg board approach to Monte Carlo Integration...
What's the Area? (Part III)
This is Part 3 of a series discussing means of calculating area (here are links to 1 and 2). This time we're going to use calculus to calculate the area of the following trapezoid.
In order to do this, we'll figure out the height of the trapezoid as a function of x. The height begins at 0.4 and increases linearly by 0.3 across the unit square. The formula for height in slope-intercept form is...
y = 0.3*x + 0.4
Next, we integrate...
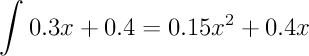
And evaluate the integral for the x in the range of [0,1]...

0.55. Calculus offers the same answer we found using geometry (i.e., looks like I didn't make any mistakes).
Q: When should we use it?
A: The calculus solution isn't as straightforward as the geometric solution; but, of course, if the top of our figure were some sort of curve, we'd probably need to move beyond geometry and on to calculus. When functions are hard or impossible to integrate, we'll need to use Simpson's Rule or Gaussian Quadrature or some other numerical integration technique. Lacking a formula for a curve, we might model the upper edge with a spline and integrate the spline to get an approximation of the actual area.
Pros: Calculus can give you answers where geometry can't.
Cons: Calculus isn't as easy as geometry.
Next, we're going to try the shotgun approach.

In order to do this, we'll figure out the height of the trapezoid as a function of x. The height begins at 0.4 and increases linearly by 0.3 across the unit square. The formula for height in slope-intercept form is...
y = 0.3*x + 0.4
Next, we integrate...
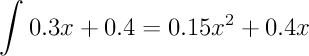
And evaluate the integral for the x in the range of [0,1]...

0.55. Calculus offers the same answer we found using geometry (i.e., looks like I didn't make any mistakes).
Q: When should we use it?
A: The calculus solution isn't as straightforward as the geometric solution; but, of course, if the top of our figure were some sort of curve, we'd probably need to move beyond geometry and on to calculus. When functions are hard or impossible to integrate, we'll need to use Simpson's Rule or Gaussian Quadrature or some other numerical integration technique. Lacking a formula for a curve, we might model the upper edge with a spline and integrate the spline to get an approximation of the actual area.
Pros: Calculus can give you answers where geometry can't.
Cons: Calculus isn't as easy as geometry.
Next, we're going to try the shotgun approach.
What's the Area? (Part II)
In the previous post, I promised to look at a few ways of determining the area of the following trapezoid. In this post, we'll look at the simplest answers, those offered by geometry.
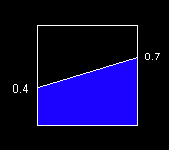
We can easily break the trapezoid up into a rectangle and a triangle.

The area of the rectangle is 0.4 * 1.0 and the area of the triangle is 0.3 * 1.0 / 2. Add them together for a total of 0.55. Simple and straight forward.
MathWorld tells us that the formula for a right trapezoid is 1/2 * a * (h1 + h2), and 1/2 * 1.0 * (0.4 + 0.7) gives us the same result of 0.55.
With little effort, geometry offered us a couple of solutions to the problem.
The geometric solution.
Q: When should we use it?
A: IMHO, whenever we can.
Pros: Simple and straightforward.
Cons: None
Next, let's look to calculus for a solution.

We can easily break the trapezoid up into a rectangle and a triangle.

The area of the rectangle is 0.4 * 1.0 and the area of the triangle is 0.3 * 1.0 / 2. Add them together for a total of 0.55. Simple and straight forward.
MathWorld tells us that the formula for a right trapezoid is 1/2 * a * (h1 + h2), and 1/2 * 1.0 * (0.4 + 0.7) gives us the same result of 0.55.
With little effort, geometry offered us a couple of solutions to the problem.
The geometric solution.
Q: When should we use it?
A: IMHO, whenever we can.
Pros: Simple and straightforward.
Cons: None
Next, let's look to calculus for a solution.
What's the Area? (Part I)
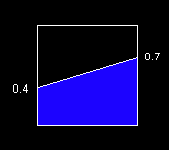
This is the first of a series of posts titled What's the Area? These posts will discuss various means of finding the area of the blue trapezoid in the following figure.
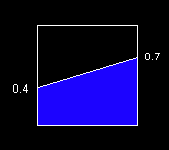
This isn't a difficult problem, and I'm going to discuss things in the simplest terms I can muster.
I don't hope to produce an exhaustive list of means of finding the area in question--just a progression of means to serve as a basis for discussion. Comments are encouraged.
To avoid confusion, let's define the problem a little more explicitly...
The blue trapezoid above is enclosed in a unit square (1 x 1). The height of its left side is 0.4 and the height of its right size is 0.7.
What's the Area?
In the next post, we'll look to geometry for a solution.

This isn't a difficult problem, and I'm going to discuss things in the simplest terms I can muster.
I don't hope to produce an exhaustive list of means of finding the area in question--just a progression of means to serve as a basis for discussion. Comments are encouraged.
To avoid confusion, let's define the problem a little more explicitly...
The blue trapezoid above is enclosed in a unit square (1 x 1). The height of its left side is 0.4 and the height of its right size is 0.7.
What's the Area?
In the next post, we'll look to geometry for a solution.
Tuesday, January 02, 2007
Free will, if I must...
Given my previous post on free will, I don't see that I have a choice but to post a follow-up link to a related NYT piece:
"Mark Hallett, a researcher with the National Institute of Neurological Disorders and Stroke, said, 'Free will does exist, but it's a perception, not a power or a driving force. People experience free will. They have the sense they are free.'
'The more you scrutinize it, the more you realize you don't have it,' he said.
That is hardly a new thought. The German philosopher Arthur Schopenhauer said, as Einstein paraphrased it, that 'a human can very well do what he wants, but cannot will what he wants.'"
link
(ht: Mr. Morty)
"Mark Hallett, a researcher with the National Institute of Neurological Disorders and Stroke, said, 'Free will does exist, but it's a perception, not a power or a driving force. People experience free will. They have the sense they are free.'
'The more you scrutinize it, the more you realize you don't have it,' he said.
That is hardly a new thought. The German philosopher Arthur Schopenhauer said, as Einstein paraphrased it, that 'a human can very well do what he wants, but cannot will what he wants.'"
link
(ht: Mr. Morty)
Monday, January 01, 2007
The Future of Computing (1994 version)
The Future of Computing: Document-Centric Computing
"Consider this e-note your electronic invitation to IBM's 'OS/2 Warp II,PowerPC & OpenDoc Sneak Peek', an exclusive and advance look at IBM's next-generation of operating systems and object-technologies, including a 'first-in-Canada' demo of IBM's new worldwide Internet service."
"OpenDoc is an open standard for document-centric computing that promises to revolutionize the way you think about your computer and its data. It is supported by Apple Macintosh, Microsoft Windows and IBM's OS/2. Future plans include UNIX, VMS and VAX"
link
"Consider this e-note your electronic invitation to IBM's 'OS/2 Warp II,PowerPC & OpenDoc Sneak Peek', an exclusive and advance look at IBM's next-generation of operating systems and object-technologies, including a 'first-in-Canada' demo of IBM's new worldwide Internet service."
"OpenDoc is an open standard for document-centric computing that promises to revolutionize the way you think about your computer and its data. It is supported by Apple Macintosh, Microsoft Windows and IBM's OS/2. Future plans include UNIX, VMS and VAX"
link
Return to Atari

Every Christmas I return to a little old farmhouse in Northern Minnesota and invariably wind up spending a little time reflecting on life.
In a closet, an old Atari 800 sits idly. Our first computer. On shelves above it, next to an old Carpenters album, are a collection of old manuals, OS source listings, software cookbooks--as you can see.
My brother and I used to write games to amuse each other. In retrospect, I'm surprised by how much we managed to learn through our autodidactic adventures in programming.
The biggest impediment to progress was a lack of information. Libraries containing books that would have been useful were at least an hour's drive. Our school was very small, offering just a couple BASIC classes. Issues of BYTE and Compute! were invaluable.
I can't help but wonder how much farther I might have gone with today's Internet at my disposal. Somewhere out there, I'm sure, there are kids learning at the speed of light.
The public good provided by the Internet in terms of information accessibility can't be understated.



