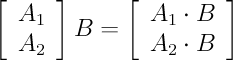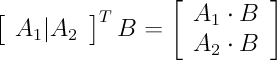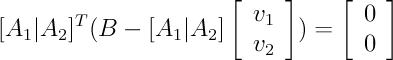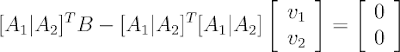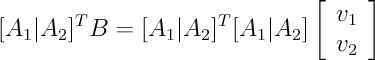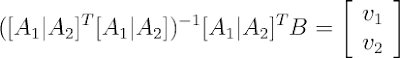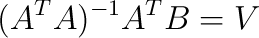The greatest soundtracks

The Guardian recently published its list of The 50 Greatest film soundtracks. Although Morricone was listed for both A Fistful of Dollars and Once Upon a Time in America, his work on Cinema Paradiso is my favorite... It's really beautiful.



Also, here's a link to the love theme from the film.

Salut

A French-themed evening, we enjoyed Avenue Montaigne (Fauteuils d'orchestre) before ambling on to Salut.

X'X inverse X'Y

If linear regression was covered in my college linear algebra class, it was covered only very briefly. Much can be said on the subject. This is post #5 in a series discussing the expression (X'X)^-1X'Y used in linear regression. Previous posts are here: #1, #2, #3, #4.

I'm grateful for the availability of Gilbert Strang's M.I.T. 18.06 lectures on video. Many thanks to both M.I.T. and Professor Strang. One of the most illuminating aspects of Strang's lectures are the different perspectives offered. He gives a masterful introduction to the properties of matrices and the associated operations from multiple perspectives: geometry, row space, column space, etc.

Seeing matrices from the various perspectives is really important, I believe. One of the things that tripped me up in my understanding of the use of matrices in linear regression was a natural inclination towards focusing strictly on row space.

Let me elaborate.

Generally, the times you find yourself in need of regression analysis look like this. There's some response surface you'd like to model. The dimensionality of the space is defined by independent variables over which you have some control, and you can sample this space by measuring some dependent response at selected points.

Following standard conventions, each point in the sample space becomes a row in a matrix typically labeled 'X' (the independent variables), and each sampled response becomes a corresponding row of another matrix typically a vector labeled 'Y' (the dependent variable(s)).

An example should do wonders. Let's consider a case using pixels on a computer screen (for the sake of simplicity assume these are greyscale pixels with an intensity from 0 to 255). The two-dimensional space of the computer screen will be sampled at various points, with the top-left pixel located at (0,0) and coordinates increasing rightward and downward.

Let's say we sample the pixels at (1,0) and (0,2) and get intensity values of 10 and 40, respectively:



We'll fit these two points with a simple linear model:

intensity = x * B₀ + y * B₁

Pixel (1,0) has an intensity of 10 and pixel (0,2) has an intensity of 40, which gives us the following two equations:

1*B₀ + 0*B₁ = 10
0*B₀ + 2*B₁ = 40

The solution to the system is obvious. Both constraints are met when B₀ is 10 and B₁ is 20.

In matrix form:

X*B = Y

Explicitly:



The system is solved by multiplying both sides by the inverse of X:



Giving the solution:



When you multiply the first row of X (the first sample point) by the coefficient vector (B), you the get the first row of vector Y; when you multiply the second row of X by the coefficient vector (B), you get the second row of Y.

The relationship between our matrices and the real world is evident. We're sampling points in a 2D space, the screen. Each point sampled corresponds to a row of the X matrix, and each sampled intensity has a corresponding row in Y.

In retrospect, an obstacle to my own understanding was the clear correspondence between the sample space in reality and the rows of the matrices. The relationship is very conducive to thinking of points in space strictly in terms of matrix rows. Unfortunately, this isn't the space in which the least squares solution exists. The rows of X are the wrong space to focus on.

"Huh? Whaddya mean it's the wrong space. It's the only space there is!"

Nope, there's another space. The rows of X are indeed points selected in your sample space (computer screen coordinates), but if you want to find the least squares solution, you need to consider the case in which the columns of X are points in space; as opposed to the "row space" of X, this is another space called the "column space."

Unlike the rows, the columns of X don't correspond directly to our real world sample space (i.e, the computer screen). Even so, the column space is where the least squares solution lives. If that seems counterintuitive and it leaves you scratching your head, don't feel alone.

I'll do my best to explain.

Let's add another pixel intensity sample to this example, except this time we'll rig the numbers so we maintain a perfect fit. We'll say the intensity at pixel (2,2) is 60, because that's what the equation we calculated above will predict: (2*B₀ + 2*B₁)= (2*10 + 2*20) = 60.



In terms of matrices, we now have three sample points in the rows of X and three intensities in the rows of Y.



Now that we have three sample points and two unknowns, we have a typical situation in which the system is overconstrained; that is, we have more constraints than unknowns, and usually there won't be a perfect solution to the system. (There's a solution for this case because we cheated in adding the fake sample with a value of 60.)

As far as matrix algebra goes, now that we've added another point, our X matrix is no longer square (it's 3 x 2), so we can no longer invert it to find a solution to the system.



Multiplying X by B gives us the following matrix-vector product:



The result is shown in what's referred to as the "row view" of a matrix-vector product. Thanks to the distributive property, we can factor B₀ and B₁ out of the result to get "the column view" of the matrix-vector product:



If you're unfamiliar with "the column view," I recommend researching it bit, because it offers valuable mathematical insights. The short answer is that the product of a matrix and a vector is a linear combination of the matrix columns. It's the first column of the matrix multiplied by the first vector component plus the second column of the matrix multiplied by the second vector component and so on. (Matrices project vectors is into their own column space.)

We can reformulate our problem in terms of the column view:



Previously we were looking at a problem involving three 2D points (pixel coordinates) and three 1D responses (pixel intensities). This is the space where our real world problem lives. Now, we've transformed this problem into one involving two 3D points and one 3D response. This is the space in which our solution lives.

Recently, I made a comment about using an Etch-A-Sketch to demonstrate linear algebra. Here's another way of asking the question: If we have an Etch-A-Sketch with two knobs, B₀ and B₁, and the first knob goes the direction (1, 0, 2) and the second knob goes the direction (0, 2, 2), is it possible to turn the knobs in such a way that you wind up at the point (10, 40, 60)? And, if so, how much do you have to turn the knobs? (We know the answer is B₀=10 and B₁=20.)

If the point closest to (10, 40, 60) lies on the surface of our imaginary Etch-A-Sketch, we have a perfect fit (which we do with our current example because we cheated). If the point is floating above or below the surface of our imaginary Etch-A-Sketch, the best we can do is move the pen to the closest possible point on the Etch-A-Sketch surface (which is what least squares does). We know how to find the solution to this problem, because we figured it out in the last post where we used linear algebra to find the projection of a vector onto a plane.

Let's spend a little time mapping what we did here to what we did there. In the preceding example, we wound up with a problem involving three points on a computer screen and three pixel intensity values. These pixel coordinates became rows in our X matrix, the unknowns became the B vector and the pixel intensity values formed the Y vector.

Next we went from the "row view" of the problem to the "column view" of the problem--a move which took us from our real world problem space to what I'm calling the "solution space." (I think it helps to think of the problem living in one world and the solution living in another.)

The column view formulation of the problem looks at the solution space and asks what combination of the two 3D vectors produces the vector Y, the one containing our three sampled intensities; and if no combination equals Y, what combination gets the closest to Y? (i.e., least squares) In other words, what is the projection of vector Y on the plane defined by all possible combinations of the two 3D vectors appearing in "the column view" of our problem?

In the context of this post* the vector B contains our unknowns. These are the coefficients we are looking to find. They will give us the best fit coefficients for predicting pixel intensities on the screen in our real world problem AND they will also give us the coefficients for the linear combination of column vectors that gets us closest to the Y vector in our "column view" solution space.

The 3D point closest to the Y vector (i.e., the projection of Y onto the column space of X) is the product X*B. In order to find the answer, we need to determine B. It may help to see the matrix product X*B, its row view and its column view again:



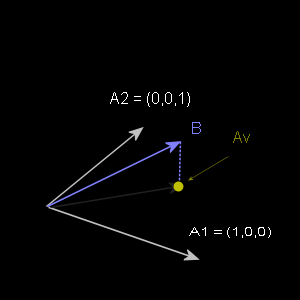
In order to find the solution, we need the vector from XB to Y perpendicular to both columns of X. This will give us the projection of Y onto the plane defined by linear combinations of the two columns of X.

The vector from XB to Y is (Y-XB). If we transpose X and multiply by (Y-XB), the result will be a two component vector containing the dot products of the columns of X with the vector from XB to Y (the point in the plane to Y). Since we want the plane perpendicular to the vector from XB to Y, the dot products must be zero. This gives us the system we need to solve:

X'(Y-XB) = [0 0]'

Now, as before, we can find the solution using matrix algebra.

distributive property:

X'Y - X'XB = [0 0]'

add X'XB to both sides:

X'Y = X'XB

and, finally, multiply both sides by the inverse of X'X:

(X'X)^-1X'Y = B

I feel like breathing a sigh of relief, because getting here was the point of this series of posts. The original question asked what's the deal with the expression (X'X)^-1X'Y used in linear regression. Hopefully, it makes more sense now. :) It's all about finding the projection of Y on the column space of the X matrix.

(Exercise for the reader. Try this in Excel, Matlab or Scilab to verify that this gives the previously calculated values, 10 and 20.)

Comments:

In this example, I simply sampled three points in a 2D space to demonstrate the differences in dimensionality of the sample space (2D) and the solution space (3D) and how they're connected to the matrix. If I'd sampled four pixels, note that we would have been working with 4D vectors and projections in the solution space. If I'd sampled five pixels, the solution space would have involved 5D vectors, and so the dimensionality vectors in the solution space increases with each additional pixel sampled.

Afewlinks...

Score one for Ray Kurzweil with Growing a Brain in Switzerland (Spiegel): A network of artificial nerves is growing in a Swiss supercomputer -- meant to simulate a natural brain, cell-for-cell. The researchers at work on "Blue Brain" promise new insights into the sources of human consciousness.

Falling flash memory prices are changing the dynamics of storage technology. (Oh, what I wouldn't give for a fast, silent drive.) Samsung announces plans to ship a 64 GB solid-state "drive."

Oh, man, Kermit is Hurt. (Edward Champion)

Apple TV is out of the gate. The hacking begins. Ars Technica reviews.

Folks have been likin' this backwards video by Mute Math. (ht: Several and sundry)

Happy Ever After

The African musical influences in Julia Fordham's Happy Ever After set it apart from other songs popular in the late 1980s. I don't feel the song ever got the cred it deserved. Thanks to the minimalistic approach taken in the video, I think it's worth watching for more reasons than eighties anthropology, and more than worth a listen--it's a beautiful song and her rich alto voice is incredible.

Her site: Julia Fordham

Atomic Confessions

At this point, I think it's time to fess up and admit it was my idea to put this Easter Egg on millions of computers. :)



It was a tongue-in-cheek response to the Photoshop 4 Easter Egg:



At the time, we were just a little shareware company. Adobe hadn't even heard of us. A few months earlier I interviewed with Adobe as well, and they said "Who?! Never heard of them!" The unknown little shareware company gave me an offer I couldn't refuse (and I always seem to wind up rooting for the little guy).

Things were pretty ragtag back then. Our artist was a talented high school student named Ben. We pitched the idea to him. He did the rest. While he was there, he came up with a lot of great creative content.

O Superman

Over 25 years after it was released, YouTube surfing kids are stumbling onto Laurie Anderson's O Superman with varied reactions and interpretations.

blondJasper: "This is the 1st time I ever saw this,I think it was banned in the UK,thanks for putting it on."

chavslayer666: "it's not banned it's just hard to find an audience for it now seeing as everyone my age was terrified of it!"

Knuth to PTO

On the question of leaving things in as good a shape as you found them, a few clippings from Donald Knuth's February 1994 letter to the Patent Office:

"In the period 1945-1980, it was generally believed that patent law did not pertain to software. However, it now appears that some people have received patents for algorithms of practical importance--e.g.,Lempel-Ziv compression and RSA public key encryption--and are now legally preventing other programmers from using these algorithms.

This is a serious change from the previous policy under which the computer revolution became possible, and I fear this change will beharmful for society. It certainly would have had a profoundly negative effect on my own work: For example, I developed software called TeX that is now used to produce more than 90% of all books and journals in mathematics and physics and to produce hundreds of thousands of technical reports in all scientific disciplines. If software patents had been commonplace in 1980, I would not have been able to create such a system, nor would I probably have ever thought of doing it, nor can I imagine anyone else doing so."

Many of today's computing industry titans skyrocketed to prominence in an industry largely free from software patents. The metaphorical beach was undeveloped. Had the previous beach dwellers been as aggressive in seeking patents, I wonder how many of these titans would have succeeded. Perhaps they would have all been sued into oblivion by mainframe and minicomputer manufacturers. The beach is different now.

Vision Puzzle Revisited

Jason Kottke posted this link to a site that claims the resolution of the human eye is equal to a 576 megapixel image. Estimates for ISO, dynamic range, etc. are also given. I can't vouch for the veracity of the site, but even an error of two orders of magnitude is enough to keep me puzzled.

Again, consider Robert Cringley's comments on the bandwidth of the optic nerve:

"What we need to emulate here is the eye, itself. Look at the optic nerve that connects the retina of your eye to the visual cortex of your brain. The optic nerve is composed of approximately one million stringy cells called ganglia that fire in parallel over a distance of two to three centimeters with the actual visual signal travelling at about 4,400 feet-per-second. Taking into account recovery time between signals, the optic nerve has a total bandwidth of approximately 100 kbps..."

How many frames per second go through the eye? I dunno. We all know when the fps is too low and things look choppy. Multiply a too slow fps by 576 megapixels. This all goes through a 100 kbps pipe? Something doesn't add up. There seems to be some killer data compression or amazing psychological tricks going on with human vision.

(Here's an old post I wrote on the subject.)

The Code of Maha'ulepu

So far I've been fortunate enough to see a few truly amazing places. The most beautiful beach I've ever visited is Maha'ulepu beach on the SE coast of Kauai.




We drove our Jeep Wrangler over bumpy private roads and then meandered through the brush to get this idyllic paradise.

Our "underground" guidebook strongly encouraged all visitors to follow a code I learned to practice generally at a very young age:

Leave the place in at least as good shape as you found it.

The book warned that abuse of the privilege might lead the owners to ban access to the site.

Judging from Flickr photos, it appears to remain pristine and undeveloped. Many residents have fought hard to preserve it.

If you're ever on Kauai, an afternoon here will be well spent.

Originally, this was going to be a post about the principle of leaving something in at least as good shape as one finds it, but that post will have to wait--the beach alone is enough to think about.

Trivial observations

The local coffee shop offers a ten cent discount to anyone who correctly answers a daily trivia question etched on a chalkboard.

Lately, this hasn't been going very well. Friday, it was the complementary color of blue. I answered with yellow. The girl behind the counter insisted it was red. Oh well, only a dime.

Today's question: "Who introduced chocolate to the Europeans?"
I answered "Aztecs."
The girl behind the counter: "No, it was Christopher Columbus."
Me: "But Christopher Columbus and his company were Europeans."
"Man, I just work here..."

I'm feeling apprehensive about tomorrow's question.

Mayans is probably a better answer.

A Flower is not a Flower

Everything appears to be on YouTube. In this case, "everything" refers to concert footage of scores of musicians I'd love to see in concert.

Following is a clip of Ryuichi Sakamoto playing A Flower is not a Flower on the piano at Tokyo International Forum Hall "C" on December 25, 2005 (according to the YouTube comment).

This is one of the most beautiful songs I've discovered over the past ten years, and if you like it, you really must hear the version played on the erhu. It will sweep you away. It well demonstrates the passion and feeling Sakamoto puts into his music.



More recently Sakamoto collaborated with Gustavo Santaolalla on the Babel sountrack.

Save the Cheerleader

With proceeds going to the Epilepsy Foundation, NBC is auctioning off a number of pieces of Heroes artwork. Paintings from Isaac's studio include the unforgettable the "save the cheerleader" painting above (titled Homecoming) as well the one featuring Hiro battling a T-Rex.

link

(ht: Drawn!)

Young Bride

Last.fm neighbor radio just played a song I'd never heard...



The wistful vocals, the determined strumming, the images and imagery, the violin... Excellent!

Midlake. Young Bride. 2006

The band, Midlake, was formed by a group of jazz students from University of North Texas. Apparently they've played SXSW a couple of times. They have other videos on YouTube. If you're interested in more, check out It Covers the Hillsides and Roscoe.

Talent Show Redux

Last year, in a post titled The Talent Show, I discussed problems I saw with PageRank and why I felt it wouldn't be the final solution in Search:

"One obvious corrective to me is a search engine equivalent of a talent show; i.e., algorithms that give search result unknowns a chance to compete for the big time. Such a strategy would involve mixing the usual results up a bit with low ranking candidates that appear to have potential. If one of these candidates is selected by users and it seems to satisfy them (i.e., they don't come back for more), the rank of the candidate could be increased."

Yesterday, I noticed Don't look now, but Google's algorithms are changing at Computerworld.

"Looking ahead, Google is going beyond site links to determine popularity, and is beginning to study the user behavior of visitors to reward or devalue sites. They gather this information in several ways. Web users who install the Google Toolbar agree that some information can be captured and forwarded to Google. If a user does a search and clicks on the third entry in the search results, Google records that the user preferred the third link rather than the first or second. It's also recording how much time a user spent on a particular site. Google can also record the computer's cache where temporary data is stored."

link

Disappearing Bees

Einstein once said that if bees disappeared we too would disappear in a few years. Unfortunately, bees are dying off in alarming numbers here in the United States and elsewhere.

---

Der Spiegel: Are GM Crops Killing Bees?

"... Since last November, the US has seen a decline in bee populations so dramatic that it eclipses all previous incidences of mass mortality. Beekeepers on the east coast of the United States complain that they have lost more than 70 percent of their stock since late last year, while the west coast has seen a decline of up to 60 percent."

---

New Scientist: Where have all the bees gone?

"It is a vanishing on the scale of entire cities. Late in 2006, commercial beekeepers in Florida began noticing alarming numbers of their bees had gone missing. Bustling colonies, tens of thousands strong, were emptying in a matter of days. Systematic searches for dead bees around the colonies mostly drew a blank.

"Bustling honeybee colonies, tens of thousands strong, were emptying in only a matter of days"

"Imagine waking one morning to find 80 per cent of the people in your community are just gone," says May Berenbaum of the University of Illinois, Urbana-Champaign.

(ht: Vision! Nary?)

Space Toy

I still need to finish up the series of posts on (X'X)^-1X'Y...

I've reached a place where I'm still trying to find of the right example for a point I want to make. In the process of thinking about this, it occurred to me that an Etch A Sketch may be good tool for teaching kids about vector spaces.



All easily demonstrated: vectors, space, orthogonality, magnitude, direction, span, linear combination, linear independence and probably many other concepts too.

Twin Peaks Season 2

If you need something to get you through the Heroes hiatus, the Twin Peaks Season 2 DVD will be available on April 3.

On Hungarian Notation...

There's no way they could have created all that amazing software without using Hungarian notation. :)

Kings of Convenience

In spite of ancestors living in the Melting Pot for generations, I'm a hundred percent Norwegian. (At least that's what my parents told me.) But I'm not sure if that can explain my fondness for a number of Norwegian artists. Still love this song.

Kings of Convenience. Misread. 2004.

And that's the links that was...

Blind kid uses echolocation to "see." Mind-blowing example of the power of the human brain. Someone needs to figure out how this kid learned to do what he does. Others could surely benefit. (link)

Stevey is funnn-nnnnnnny! Okay, Mr. Yegge, you've won me over. Recently posted journal entries from his first weeks at Google in 2005, A Noogler's View of Google: "I mean, come on, it's pretty obvious they're going to eat us. Geez, we've all read fairy tales before. Nobody just gives you a bunch of free food for as long as you want without killing you and eating you. Like, duh. But I can vouch for Kirkland: when the Feasting Day OKR comes around, we'll be ready. I myself would probably go well with cranberry sauce." (link)

Crystal Cave of Giants in Mexico. These are the largest cave crystals I've ever seen. Is that Marlon Brando in the background? Jor-El... Jor-El??? (link)

Brad DeLong's Morning Coffee: "Income inequality in America has taken an enormous leap upwards since the mid-1980s, leaving us today with a society that is as unequal as America was in the pre-Great Depression Gilded Age." (link)

Ars Technica Digs into Vista. "This is Part I of Ars Technica's three-part Windows Vista review coverage. In the coming weeks we will be expanding on this coverage, culminating in an official review when our testing is finished. For now, let's get under the hood..." (link)

Foresight Exchange. "A notional stock market where you buy shares betting on the outcome of future events." (link)

Javascript Closures. I used to be a real computer language hound, but I reached a point of diminishing returns in terms of interestingness. Lately, I've been playing catch up. Javascript, the language of the browser, is a much cooler language than I realized. It even supports closures. (link)

Web 2.0 Adoption. Nicholas Carr: "Yesterday, Forrester released some results from a December 2006 survey of 119 CIOs at mid-size and larger companies. It indicated that Web 2.0 is being broadly and rapidly brought into enterprises. Fully 89% of the CIOs said they had adopted at least one of six prominent Web 2.0 tools - blogs, wikis, podcasts, RSS, social networking, and content tagging - and a remarkable 35% said they were already using all six of the tools." (link)

On the Artistic Side. If you need an art fix, check out the great work of Thomas Ehretsmann, especially the Illustration section. (link via Drawn!)

(this is the 3rd post I've lost and had to retype thanks to the behavior of the new Blogger.)

Averaging One Redux

Last month I made a comment about the questionable sorting user ratings in the post: Averaging One. Today, Aleks at Statistical Modeling came to the rescue with "Bayesian sorting by rank." (Thanks, Alex! Now I have one less puzzle to think about.)

Blogs

When I see a lot of blogging about blogging, I begin to feel something's gone terribly wrong, so I try to avoid the practice altogether. This time, however, I'm going to make an exception.

Recently, Nicholas Carr offered up a biting post on the subject of Twitter (an entity to which I'll confess not getting as well); in the comments, he left a link to a piece by Geert Lovink quite critical of blogging as well:

"As a micro-heroic, Nietzschean act of the pyjama people, blogging grows out of a nihilism of strength, not out of the weakness of pessimism. Instead of time and again presenting blog entries as self-promotion, we should interpret them as decadent artifacts that remotely dismantle the mighty and seductive power of the broadcast media. Bloggers are nihilists because they are "good for nothing". They post into Nirvana and have turned their futility into a productive force. They are the nothingists who celebrate the death of the centralized meaning structures and ignore the accusation that they would only produce noise."

Introspection ensued.

What am I doing? What are you doing? Why do I do I write this blog? Why do I read your blog?

It's hard to come to just a few simple answers. I feel I could write a great deal on the subject.

I subscribe to several blogs for a variety of reasons. If there's a common strand linking them all together, perhaps it's an admiration for the intellect and talent of the authors.

With some blogs, it's a matter of specialized, common interests. The MSM, for example, doesn't tend to write many articles targeted at readers interesting esoteric mathematical topics or learning how to start a fire in the wilderness with a soda can.

Along similar lines, I read several blogs written by academics outside or on the fringes of my own field. Attempting to plow through a paper written outside your own field can easily fail to meet the requirements of fun, but academic blogs are often written in a casual style; not only can they give one a feel for what's going on in a particular discipline, they are often very informative and educational.

There are a number of smart individuals and great thinkers doing a lot of great writing in blogs. Given the general lack of profitability of blogs, the motivations of many bloggers seem purer in comparison to other media where profit motives are more intense.

RSS feeds make it easy to aggregate a disparate choir of thinkers into a single medium. Reading the words of intelligent people appoaching problems from a variety of angles is one of the better means I've found at getting to the truth--or at least trying to do so.

If blogs disappeared, how would I fill the void left behind? I'm not sure I could. In some cases, I could find substitutes to the lost writers, but in other cases, I think it would be difficult or impossible to find replacements. In the case of academic blogs, I could subscribe to journals, but, again, they'd be targeted at professionals inside the various disciplines and the reading would be heavy. In other cases, blogs would probably be impossible to replace due to their degrees of specialization or their very unique blends of subject matter.

There's a phenomenon for which I'm not sure I've yet seen a term--"self-classification," perhaps. People who like the same old things often like the same new things. Even before the existence of Last.fm, I often found myself searching Google for, say, "Band #1" and "Band #2" working on the assumption that if there's anybody in cyberspace liking both, there might be other things on their lists I like as well. The strategy worked--I found a lot of great music by doing just that.

This self-classification strategy works with blogs as well. Find some blogging geek who likes cooking, P.G. Wodehouse and cave diving as much as you, and he or she will probably wind up blogging about other things you find interesting too. This isn't even a "micromarket." It's more like a "nanomarket."

This is getting too long. Even though there's more to say, I'm going to stop writing for now, but I'll continue to think about it.

Biology & Morality

The relationship between biology and morality is an area of personal interest. It seems it's impossible to discuss the subject without seeing the names of David Hume, Immanuel Kant and E.O. Wilson, and this NYT article reinforces the claim.

I'm neither a professional philosopher nor a biologist, but it does seem to me that discussions such as this often present a false dichotomy between emotion and reason.

Such analysis seems too simplistic, linear and blind to feedback loops. Emotion leads us to reason, the reasoning leads to new emotions, the new emotions lead to new reasoning and so on.

link

Virtual Beauty

There's an interesting post at Statistical Modeling... on research into the classification and synthesis of facial beauty. The first part mentions work by Australian researchers who created classification software devoted to answering the question "fairest of them all?" The second part points to an older German study that concluded that the most beautiful faces don't and can't exist:

"Having these results in mind it is also not surprising that a model agency from Munich chose 88% artificial faces (14 out of 16 selected faces) for potentially being interesting as a model for the category “beauty”. Only two natural male faces could keep up with the computer generated ones, within the group of female faces no natural faces have been selected! We also asked test subjects to indicate the most attractive faces found the same pattern: 81% (13 out of 16) of the selected faces had been generated by the computer.

I do know Mandinka

There are a number of videos to which I've planned on posting links. Unfortunately, it seems, Viacom has pulled the plug on that party. At this end, I'm not seeking to make a dime off anyone else's work. I'm simply trying to promote great artists and notable achievements. It's unfortunate.

One of the vids on my list was Mandinka by Sinead O'Connor from 1987. If my sources are correct, she hasn't even sung this song in concert for a long time.

I think it's her best song, and it's one that showcases her amazing vocal range. How many female artists can slide through that many octaves? Wow!

Here's her performance of the song at the 1989 Grammy's.

Linked List? Now patented!

According to Grady Booch, Ming-Jen Wang of LSI Logic Corporation, with the help of a patent examiner, has patented the linked list (link). Grrr.

The New Blogger

Both Google and Yahoo! seem hell-bent on mainstreaming acquired users into their systems. In the case of Yahoo! this has affected me as a Flickr user. In the case of Google, the suffering is due to my being a Blogger user.

To their credit, at least Google offered a new version of Blogger as a carrot to get me to switch. As far as I can tell, Yahoo! has simply said "My way or the highway!"

The new Blogger? As far as it goes, I'm becoming exceedingly frustrated with it. Twice I've incorrectly entered a garbled Captcha while posting. The consequence is a rejection screen. I've found no course of action other than clicking the Back button on my browser. The result? My post has been devoured by the bit bucket--a half an hour's worth of work down the drain--utterly kablooey.

Nice...

(Copying this post to the clipboard in case it happens again...)

Yet Another Face

YetAnotherFace is a sub-brand name for the 3d illustration style of Petra Stefankova. Born and raised in Slovokia, Petra is a graphic designer and illustrator currently living in London.

"At the beginning there was an idea to move the surrealist automatic drawings produced since 1999 a step further and bring them into another dimension... with this idea first four 3D CGI artworks came in a series."

(Very cool concept and style!)

link

(ht: Drawn!)

Feynman Messenger Lectures

"As part of Cornell University's Messenger Lecture Series in 1964, professor Richard Feynman delivered a series of seven lectures on physics and the process by which quantum theory was developed."

via Google Video

Lecture 1 - The Law of Gravitation
Lecture 2 - The Relation of Mathematics and Physics
Lecture 3 - The Great Conservation Principles
Lecture 4 - Symmetry in Physical Law
Lecture 5 - The Distinction Between Past and Future
Lecture 6 - Probability and Uncertainty
Lecture 7 - Seeking New Laws

----


Update:

Sigh. I think there's a rule in online digital media that goes "All good things must come to an end." Unfortunately, it seems the videos have disappeared. (Should have downloaded them while I had the chance.). Oh well, perhaps some day they'll reappear.

The U.S. Constitution provides the moral justification for protecting copyright (i.e., why do we as a society even bother with protecting such things?):

"To promote the Progress of Science and useful Arts, by securing for limited Times to Authors and Inventors the exclusive Right to their respective Writings and Discoveries."

I often wonder to what extent science and arts are being promoted these days.

To the limit one more time...

For the first time in quite a while, computers are hitting a limit in terms of addressable memory. Without playing any tricks, the limits of today's 32-bit systems is 4 gigabytes (2^32).

Perhaps this is the last time we'll hit such a limit, but I think the idea of hitting this limit would have been inconceivable in the days of of the Apple II and other 8-bit systems.

If you back up far enough on Computer Memory Lane, you'll run into this critter, a 16K-RAM cartridge for the Atari 400 and 800 computers introduced ~1979.



As a kid, I remember always wishing I had another $300 (?) to plunk down on one of these babies. I don't have the specs, but these cartridges were about 6-8" wide, 4" high and about 3/4" thick. Maximum addressable memory: 65,536 bytes (RAM + ROM).

Below is today's 2.0 GB SD card. It's smaller than a matchbook, and you can get one for around $30. If you stack those old Atari 16K-RAM cartridges a mile high, you still won't equal it in terms of capacity.



Next, we move on to 64-bit computing. The memory limit this time is 1.84467441 × 10¹⁹. That's an incomprehensibly huge number, on the order of a 100 MB for each brain cell inside your head.

Game [Show] Theory

Recently, the first 3-way tie in the history of Jeopardy occured. I found a YouTube link for it here. The two trailing contestants were tied for $8,000 dollars. The leader bet $2,600 resulting in $16,000 for each of the three contestants.

Most interesting (and insulting, actually) are many of the YouTube comments disparaging the winning player for not winning, but it seems quite clear to that the leader bet fully aware, and quite possibly hopeful, of the game ending as it did.

Judging from facial expressions, I think some of it was altruistic, but I think a good case can also be made for it being a rational choice as well. Is it really worth earning one more dollar and winning, if it means giving up a decent chance of replaying two players who are known quantities already defeated once?

Seems to me spending $1 to play two players you already beat is a reasonable expense.

Update: I just stumbled onto some interesting coverage of this at Lance Fortnow's Computational Complexity.

The Lives of Others

Das Leben der Anderen won the 2007 Oscar for best foreign film and many other awards. In 1984 East Germany, the Stasi surveils a playwright and his lover. This is one of the best films I've seen in a very long time.

Vector projection on a plane

This is post #4 of a series discussing the expression (X'X)^-1X'Y used in multiple linear regression. (Here are links to earlier posts: #1, #2, #3).

Last time we projected a 2D vector onto a 1D subspace (a line). This time we'll project a 3D vector onto a 2D subspace (a plane). In the image below, all vectors are 3D and B will be projected down onto the plane shared by A1 and A2. Again, Av is the point of projection, the result of the orthogonal projection of B on the plane.



Previously, we solved for a case in which (B - Av) and a single vector A were orthogonal (their dot product was zero). This time we need to solve for the case in which (B - Av) is orthogonal to two vectors, both A1 and A2. This will give us the point, Av, of the orthogonal projection of B onto the plane defined by A1 and A2. Given our need for a simultaneous solution to both linear equations, this is a job for linear algebra.

Multiplication of matrices amounts to calculating dot products of matrix rows and matrix columns--the rows come from the first matrix and the columns come from the second matrix.

For example, if we put A1 in the first row of a matrix and A2 in the second row, we can use matrix multiplication to calculate the dot products A1 . B and A2 . B as follows:



In order to get results in the form we expect to see, however, we'll put A1 and A2 into columns of the first matrix and multiply the transpose of this first matrix by B. This won't affect the calculations, just how things are displayed.

The following is mathematically equivalent to the previous equation (a matrix with A1 and A2 as row vectors is the same as the transpose of a matrix that has A1 and A2 as column vectors):



Note: I've added a vertical bar between A1 and A2 to indicate they are column vectors of the matrix.

In order to find the projection of vector B onto the plane, we need to solve for v1 where A1 . (B - A1 * v1) = 0 and we need to solve for v2 where A2 . (B - A2 * v2) = 0. We can express both linear equations together in the following matrix equation:



It may be helpful to refer back to the previous post, because this example is designed to mirror the previous simpler example as much as possible. In the previous post, we solved a dot product equation. We're doing the same thing here, except we have two dot product equations this time, and we're using linear algebra to solve them both simultaneously.

Just as we used the distributive property of algebra before, here we use the distributive property of matrices to get A . B - A . A v:




Add A . Av to both sides:



Again, we multiply both sides by the inverse of A . A (but this time we use a matrix inverse):



At this point, it will be probably be a little clearer if we simply use 'A' to refer to the matrix with column vectors A1 and A2 (and V for the matrix containing v1 an v2):



The point of this series of posts is explaining the story behind the (X'X)^-1 X'Y found in multiple linear regression. The expression above is the same except X and Y have been replaced with A and B to avoid confusion with Cartesian coordinates. Half the story is multiple linear regression finds its solution through a vector projection. We'll explore this in greater depth in the next post.

Finally, as was the case in the previous post, we need to multiply A by V to get the projection of vector B onto the plane defined by A1 and A2.



As before, there are bonus prizes. Now you know how to find the distance from a point to a plane and exactly where the nearest point on the plane lies. Furthermore, because we've the projection problem into the world of linear algebra, the same equations work in higher dimensions (4D, 5D and beyond).

Next time, we'll investigate the relationship between vector projection and multiple linear regression in greater detail.

A simple vector projection

This is post #3 of a series discussing the expression (X'X)^-1X'Y used in multiple linear regression. (Here are links to earlier posts: #1, #2).

In the last post, we showed the dot product of two orthogonal vectors is zero. This time we'll leverage that knowledge to find the orthogonal projection of one vector onto another another.

If you're following along and you're not sure what an orthogonal projection is, the following figure should be helpful.



Given vectors A and B, we're going to find the point on vector A that's closest to point B. The shortest possible path from B to A is the line perpendicular to A that also intersects B, hence "orthogonal projection."

Because the point is somewhere on A, it can be expressed as A multiplied some scalar 'v'. I've labeled it 'Av' above. We'll find a solution by determining the value of 'v'.

Since we know the dot product of orthogonal vectors is zero (last post), we know that the dot product of vector A and the vector from Av to point B must be zero as well, which gives us:

A . (B-Av) = 0

(I'm using a period '.' to indicate dot product.)

Because dot product is distributive, we can change the equation to:

A . B - A . Av = 0

Adding A . Av to both sides gives us:

A . B = A . Av

And because dot product is associative for scalars:

A . B = (A . A)v

Solving for v by multiplying both sides of the equation by the inverse of (A . A):

(1 / A . A) * (A . B) = v

We've found 'v'.

Since the projection of B on A is A*v, we multiply them for the solution:

proj_A(B) = A*v = A (1 / A . A) * (A . B)

The utility of this goes beyond the context of this series of posts. You can use this technique to find the shortest distance from a point to a line and exactly where that nearest point on the line actually is.

Next, we'll extend the idea and project a vector onto a plane.

Dot products of orthogonal vectors

This is post #2 of a series discussing the expression (X'X)^-1X'Y used in multiple linear regression. Post #1 is here.

If you have two vectors that are perpendicular to each other (i.e., orthogonal), their dot product is zero. I'm going to devote this post to convincing us of this fact.

The dot product of two vectors is the sum of the products of all of the corresponding components of those two vectors. It applies in any number of dimensions. In the two dimensional case, the dot product of vectors U and V is U_x* V_x + U_y* V_y.

First, let's see if this works in the simplest case I can imagine, the case of a unit vector pointing up (0,1) and another unit vector pointing to the right (1,0). The dot product of these two vectors is 0*1 + 1*0, which is, of course, zero.



Next, let's rotate our two unit vectors by some angle theta and see what we can conclude.



Our "up" vector rotates from (0,1) to (-sinq, cosq) and our "right" vector rotates from (1,0) to (cosq, sinq).



The dot product of the rotated vectors is (-sinq*cosq + sinq*cosq). Since the first term negates the second, we can see that the dot product remains zero regardless of rotation.

Now that we've shown the dot product of our two perpendiculars vectors is zero regardless of their rotation, we have two more degrees of freedom to consider. So far we've constrained our vectors to unit length.

Finally, let's scale our first vector by A and our second vector by B. This leaves us with two vectors: (-A*sinq, A*cosq) and (B*cosq, B*sinq). The dot product of these two vectors is (-A*B*sinq*cosq + A*B*sinq*cosq). Once again, the two terms negate each other and result in a sum of zero for all possible combinations of A and B.

Speaking more generally, the dot product of two unit vectors is the cosine of the angle between them. This rule holds true with the orthogonal vectors we just discussed, because the angle between orthogonal vectors is 90 degrees (pi/2) and the cosine of 90 is zero.

Up next: A simple vector projection

Why X'X inverse times X'Y?

If you ever wind up calculating multiple linear regression yourself, you'll undoubtedly run into (X^TX)^-1X^TY, a cryptic looking expression which might be mistaken for a magic word from an old adventure game.

What's the story behind the magical expression(X^TX)^-1X^TY? What is it? How did it get that way? These are some questions I'll take a stab at answering in upcoming posts.

Next: Dot products of orthogonal vectors.

Accidental Creation #47

Sometimes in the course of testing various pieces of code I've written, I wind up creating accidental works of art. This is the first "work" I've showcased here, but I'm calling it Accidental Creation #47.

Moonlight spills on comic books...

Standing Outside a Broken Phone Booth with Money in My Hand.
Primitive Radio Gods. 1996

Noisy Apartment Building

My father loves fishing. A major appeal for him, I believe, is serenity. Drifting quietly in some remote bay, it's a tranquil escape from telemarketers, family squabbles, nagging and the interruptions inherent in daily life.

Most of us who don't fish have some equivalent form of escape. For example, rather than a remote Northern lake, my escape usually entails diving into a computer screen. I find it easy to be blissfully swept away by computing problems and a never-ending flow of knowledge and fascinating news.

Unfortunately, my computing experience is becoming progressively less and less blissful. In contrast to a quiet lake, it's becoming more and more akin to living with my mother in an urban apartment building with a bunch of bickering children.

Let the Wayne's World dream sequence begin...

Child #1: "Dad?"
Me: "What?"
Child #1: "Dad, can I play your mp3s?"
Child #2: "No, I wanna play your mp3s!"
Child #3: "You said I could play your mp3s, and he took them. Can I take them back?"

Child #4: "I wanna download your pictures!"
Child #5: "No, I wanna download your pictures!"

I think I just heard my mother.
"Mom?"
"Son, we need to clean up your room. You have unused icons laying all over the place."
"Just a second. I need to bat a couple tooltips and get the door."

Door.
"Hello?"
"Hi, I'm from Microsoft, building maintenance. Is it okay if I come in and fix a few things."
"Weren't you here just last week?"
"Um, yeah, this is something else. Need to set the building clocks... and we need to change your locks."
"I thought you changed the locks last week. I hope you're not going to make me leave the building and come back in again..."
"Um.... Nope, no fire drills this time..."
"Whatever. Come on in."

"Mom?"
"The icons!"
"Yeah, I know, but I'm okay with the mess. Sorry. Door again."
"Hello?"
"Hi, I'm from the PDF viewer company. Need to do a little fixer upper on your PDF-ef."
"Fine. Come in."
"Son?"
"Yeah, Mom."
"I brought your mail in. There's about 700 lbs of it. A lot of it is stock tips."
"Yeah, I know."
Door again.
"Hello? Not you again. No, I don't want to punch the monkey!"
"Son?"
"Yeah, Mom."
"Why are you putting your coat on?"
"Because I'm leaving!"
"Where are you going?"
"Fishing..."

I Say, and So Say I

I noted the song beginning "I say, and so say I ..." in the new J.C. Penney commercial is "What Can it Be" by Forever Thursday. Thanks to a commenter for noting the voice belongs to Australian singer Melanie Horsnell.

I'm revisiting this because it's clear from my hits a lot of people would like an answer to this question, and Google's sending people to my main page.

You can hear the song on the Forever Thursday website (ForeverThursday.com) and on the Forever Thursday MySpace page. You can hear more from Melanie Horsnell at her site, MelanieHorsnell.com and the Melanie Horsnell MySpace page. You can also pick up a copy of the song on iTunes.

Enjoy!

Bit hack puzzle

A few times I've found myself writing code to threshold greyscale images. In cases where I've really needed performance, I've used MMX and SSE, but yesterday, in the process of running some tests, I wrote a quick implementation in C++ that boiled down to this...

for all pixels in image
{
   pixel = pixel < 128 ? 0 : 255
}

It dawned on me that there's a bit hack for this, but I've never seen anyone mention it. If you want the answer, select the next line with your mouse:

pixel = (unsigned char) -((char)(pixel>>7))

Fessin's of a [would be] Ad Man...

Lately, there's been a lot of great advertising going on...

I love The Martin Agency's Geico Caveman, of which one of the most recent, Caveman at the Airport, includes Royksopp's excellent Remind Me. (Also, here's a link to the very cool video of a more techno-esque remix: link).

TBWA/Chiat/Day's "Mac vs. PC" ads have been some the best of the decade. Cramer-Krasselt keeps cranking out one hilarious CareerBuilder.com ad after another.

And if you're trying to figure out who sings the tune that begins "I say and so say I..." in the latest J.C. Penney ad, the song is How Can it Be by the Australian group Forever Thursday.

Bravo to all!

Until I'm proven wrong, I'm going to claim I'm the only computer science major who ever considered switching to advertising :)

Principles from X

Occasionally I run into beautifully and succinctly stated software design truths. These are from Scheifler & Gettys: The X Window System:

Do not add new functionality unless an implementor cannot complete a real application without it.

It is as important to decide what a system is not as to decide what it is. Do not serve all the world's needs; rather, make the system extensible so that additional needs can be met in an upwardly compatible fashion.

The only thing worse than generalizing from one example is generalizing from no examples at all.

If a problem is not completely understood, it is probably best to provide no solution at all.

If you can get 90 percent of the desired effect for 10 percent of the work, use the simpler solution.

Isolate complexity as much as possible.

Provide mechanism, rather than policy. In particular, place user interface policy in the client's hands.

I Saw the Light

The video streak continues...

This is Lori Carson (Golden Palominos) remaking Todd Rundgren's I Saw the Light. 1997

Possibilities

Product improvement thoughts...

Digital thermometer

I have a digital thermometer that tells me when the meat is done, but there's something about it I don't like. It slowly climbs to the final temperature as the probe absorbs surrounding heat (In retrospect, I worry about Google referrals I'll get for that sentence). Given the first few samples, I think it should be able to provide a reasonably accurate estimate of the final temperature much more quickly. If there's a rare pork liability issue, have it beep once it hits some confidence level.


Thumb drives

I'd like to use my thumb drive as a replacement for a coffee card. (Maybe even all my cards, if it can be done in a reasonably secure manner). And I also want to be able to store a definition of "the usual" on this thumb drive, because coffee orders have gotten too complicated. Let me hand you my thumb drive and say, "I'd like 'the usual'."


Automatic teller machines

Here's a machine learning problem waiting for a solution. When you can get a gig of flash memory for $20, maybe it's time to create ATMs that remember if I speak English or Spanish and also remember that I pretty much always either make a deposit or withdraw $100. Ideally, the mothership should remember this for all machines, but I've given up on that ever happening. I'll even be happy if it's merely remembered by individual machines. A gig should be way more than enough for a machine to remember every customer it will ever have. And, why oh why, must the user interface on these machines require a search through four levels of menus? Most of these machines could be inducted into a user interface hall of shame.


Universal power cords

Game boys, cell phones, laptops, etc., etc., etc. How many things do I have in my household that need to be recharged? And how much I wish I could have fewer cords around! How about a smarter power cord that can recognize how much juice a device needs and pipe it through a standard connector? If Honda can build a robot that jogs...


Small Laptop Expansion Bay

Given how tiny they can make dongles for wireless mice, Bluetooth and Wi-Fi and thumb drives, a little bay for a few small USB2 devs would be a really welcome laptop feature. With plummeting flash memory, there's a potential for high speed flash fun with RAID 0.


Compact Disc packaging

I've had a lot of trouble with the packaging of newly purchased CDs just falling off by itself. This results in many a scratched disc. The packaging needs to be more robust and harder to get off. I think an iron box completely welded shut might be the answer.

Hit

Hit. The Sugarcubes. 1991

Got Snow?

Quite some time has passed since snow has fallen in such abundance. Inch after inch fell straight from the sky for more than two days--so serenely that snowflakes have been beautifully stacked in ways I don't believe I've ever seen. Above, you can see +12" accumulated on the railing of my deck. It's even stacked like this on the branches of the trees.

Can't Be Sure

Can't Be Sure by The Sundays. 1989