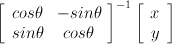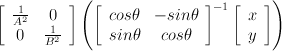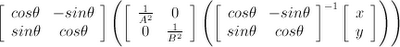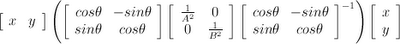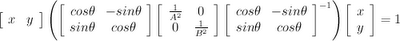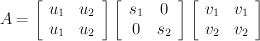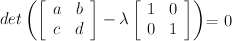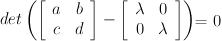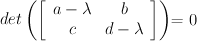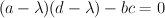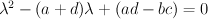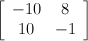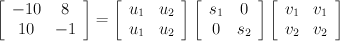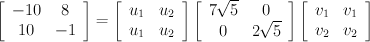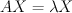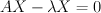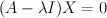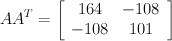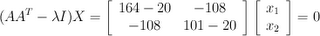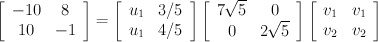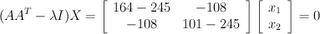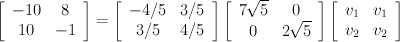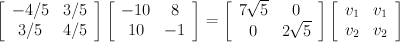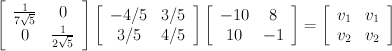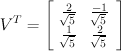I have been getting a surprising number of Google referrals from people wondering how to calculate the SVD of a 2x2 matrix by hand. The number of hits is surprising because I haven't answered this question, and now I'm feeling compelled to answer it.
Calculating the SVD of even a 2x2 by hand is sort of tedious, so maybe what I need to do is start writing about the subject, post that start and hope a sense of duty will compel me to finish it.
On
this page, Todd Will calculates the SVD of this matrix by hand using other means. If you want a shorter way to do it, I recommend you go there. What I'm going to do here might be called "the long way," but I'm feeling like a glutton for punishment, so here goes...
In
this post, I talked about the U containing the eigenvectors of AA
T , V containing the eigenvectors of A
TA and S containing the square roots of the eigenvalues.
If you want to calculate the SVD of a 2 x 2 matrix, one way to do it is to start by calculating the eigenvalues of A
TA and AA
T (they share the same eigenvalues).
To calculate the eigenvalues of a 2 x 2, you need to solve this equation:
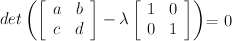 Multiplying out lambda leaves you with
Multiplying out lambda leaves you with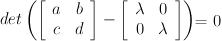 Matrix subtraction leaves you with
Matrix subtraction leaves you with 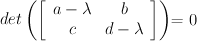 Calculation of the 2x2 determinant leaves you with
Calculation of the 2x2 determinant leaves you with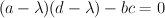 Expanding that leaves you with
Expanding that leaves you with 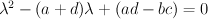
This is a quadratic you can solve via the
quadratic formula by substituting 1 for a, -(a+d) for b and (ad-bc) for c.
Consider the following 2 x 2 matrix.
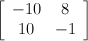
Let's use this matrix and see if the method I'm using here brings us to the same results. If we succeed you'll have two means of calculating SVD by hand.
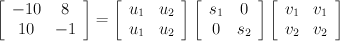
I'll do the work in Scilab:
-->A=[-10 8; 10 -1] A =
-10. 8. 10. -1. -->AA=A*A' AA =164. -108. -108. 101.-->z = [164*101-(-108)*(-108) -(164+101) 1] z =
4900. - 265. 1.
-->q=poly(z,'x','coeff')
q =
4900 - 265x + x^2
-->roots(q)
ans =
20. 245.
The eigenvalues of AA
T are 20 and 245, or 2*sqrt(5) and 7*sqrt(5). These are also the eigenvalues of A
TA, but I'm not going to work it out here. Finally, the square roots of these values form the elements on the diagonal matrix S in our SVD of A, so they'll return later when we put the whole thing together.
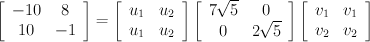
Now that we have the eigenvalues of AA
T, we can calculate its eigenvectors. In quick review, an eigenvector is a vector whose direction doesn't change when it's transformed by its matrix. When matrix A transforms its eigenvector X, the length of X may change, but the effect of the multiplication is nothing more than a scaling of X. The scaling factor is the eigenvalue, and it's usually designated with the symbol lambda.
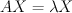 Subtraction gives us
Subtraction gives us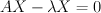 Factoring out X gives us
Factoring out X gives us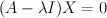
Earlier (in Scilab) we calculated AA
T and its eigenvalues, 20 and 245.
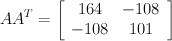
First, we'll plug AA
T and 20 into the previous equation.
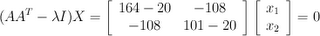
The product results in these equations.
144*x
1 - 108*x
2 = 0
-108*x
1 + 81*x
2 = 0
You might be habitually inclined to seek a unique solution to the system, but we're looking for a vector rather than a point. The two equations are equivalent, and we can find the relationship between x
1 and x
2 by looking at either. Let's simply look at the first equation.
144*x
1 - 108*x
2 = 0
144*x
1 = 108*x
2x
1 = 108/144*x
2x
1 = (3/4)*x
2Any multiple of (3/4, 1) should satisfy the equation. Since we'd like the vectors to be unit length (see
SVD and orthonormal bases), let's normalize the length of the vector.
Following the
Pythagorean theorem, the length of (3/4, 1) is the square root of the following:
sqrt((3/4)
2+1
2) = sqrt(16/16 + 9/16) = sqrt(25/16) = 5/4
It's nice how that worked out.Our unit length eigenvector is:
(1/(5/4))*(3/4, 1) = (4/5)*(3/4, 1) = (3/5, 4/5)
We have one of the four eigenvectors we need to calculate.
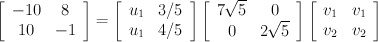
Next we return to the other eigenvalue, 245, and plug it into our eigenvector equation.
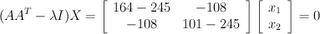
This time we get
-81*x1 -108*x2 = 0
-108*x1 -144*x2 = 0
Looking at the first equation again
-81*x1 -108*x2 = 0
-81*x1 = 108*x2
x1 = -108/81*x2
x1 = -4/3*x2
This time our eigenvector solution is (-4/3, 1), which we'll normalize below.
Find the length of the vectorsqrt((-4/3)*(-4/3)+1*1) = sqrt( 16/9 + 9/9) = sqrt(25/9) = 5/3
Again, scale by 1/length(1/(5/3))*(-4/3,1) = (3/5)*(-4/3,1) = (-4/5, 3/5)
So now we've have unit length eigenvectors of AA
T:
(3/5, 4/5) and (-4/5, 3/5).
AA
T is symmetric and the eigenvectors of a
symmetric matrix are orthogonal, which means their dot product is zero. This is clear by looking at them, but I'll multiply it out, because this post is all about being verbose:
(4/5, 3/5) dot (-3/5,4/5) = (4/5)*(-3/5) + (3/5*4/5) = -12/25 + 12/25 = 0
Let's add our other eigenvector to the first column U. It corresponds to the largest eigenvalue and the top-left "singular value" in the S matrix.
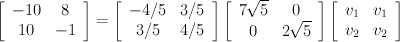
Now that we've calculated U and S, we can solve for V. In doing this, I'm going to exploit some of the properties of U and S.
First, let's multiply the left sides of both equations by the inverse of U. If you recall, because U is an orthogonal matrix, its inverse is its transpose, so we simply need to multiply the left side of the equation by the transpose of U to eliminate U on the right side. In this case, U happens to be symmetric, so it's also its own transpose (that won't always be the case).
A = U*S*V
T =
U
-1*A = U
-1*U*S*V
T =
U
-1*A = S*V
T =
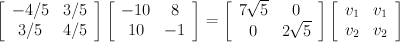
Multiplying both sides by the inverse of S will leave us with V
T on the right side. Because S is a diagonal matrix, the inverse is calculated by replacing each element on the diagonal with its reciprocal.
U
-1*A = S*V
T =
S
-1*U
-1*A = S
-1*S*V
T =
S
-1*U
-1*A = V
T =
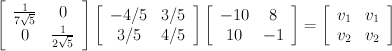
Multiplying everything out leaves us with the following:
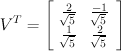
At this point we know U, S and the transpose of V. Putting everything back together leaves us with:
A = U*S*V
T =

Update (1/12/2007): If you're reading this, you may be interested in Jim Blinn's paper titled
Consider the Lowly 2x2, which you can find on IEEE or in his book
Notation, Notation, Notation.
If you want to write a program to calculate the SVD, don't infer the algorithms from this post; sound computational means are found in the classic text
Matrix Computations by Golub & Van Loan.
This is post #12 of Linear Algebra for Graphics Geeks. Here are links to posts
#1,
#2,
#3,
#4,
#5,
#6,
#7,
#8,
#9,
#10,
#11.
Next, some commentary on matrices, elipses and eigen decomposition.